
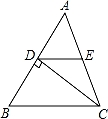
如图,△ABC中,CD⊥AB于D,E 是AC的中点.若AD=6,DE=5,则CD的长等于 .
是AC的中点.若AD=6,DE=5,则CD的长等于 .
科目:初中数学 来源: 题型:
学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
| 解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
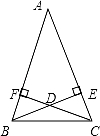
A.① B.② C.①② D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
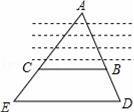
如图,在河两岸分别有A、B两村,现测得A、B、D在一条直线上,A、C、E在一条直线上,BC∥DE,DE=100米,BC=70米,BD=30米,求A、B两村间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com