下列图形中，是轴对称图形但不是中心对称图形的是（ ）
A．等边三角形 B．平行四边形 C．矩形 D．圆
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案科目：初中数学 来源： 题型：
二次函数y=ax2+bx+c（a、b、c为常数，且a≠0）中的x与y的部分对应值如下表：
| x | … | 0 | 1 | 2 | … |
| y | … | 4 | ﹣4 | 6 | … |
（1）ac＜0；（2）当x＞1时，y的值随x值得增大而增大；（3）﹣1是方程ax2+bx+c=0的一个根；（4）当﹣1＜x＜2时，ax2+bx+c＜0，其中正确的个数为( )
A．4个 B．3个 C．2个 D．1个
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，抛物线y=a（x﹣1）2+4与x轴交于A、B两点，与y轴交于点C，M为抛物线的顶点，直线MD⊥x轴于点D，E是线段DM上一点，DE=1，且∠DBE=∠BMD．
（1）求抛物线的解析式；
（2）P是抛物线上一点，且△PBE是以BE为一条直角边的直角三角形，请求出所有符合条件的P点的坐标；
（3）如图2，N为线段MD上一个动点，以N为等腰三角形顶角顶点，NA为腰构造等腰△NAG，且G点落在直线CM上，若在直线CM上满足条件的G点有且只有一个时，求点N的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
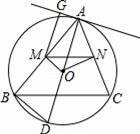
已知：如图，△ABC是⊙O内接三角形，OM⊥AB于点M，ON⊥AC于点N，连接MN，
（1）求证：MN=
BC；
（2）过点A作⊙O的直径AD，连接BD，AG为过点A的圆切线，过点M作MG⊥AG，垂足为G，若cos∠BAD=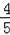
，BD=20，求AG的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（ ）
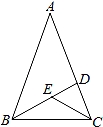
A．5个 B．4个 C．3个 D．2个
查看答案和解析>>
科目：初中数学 来源： 题型：
某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，其图象如图所示．当气球内气体的气压大于150kPa时，气球将爆炸．为了安全，气体体积V应该是（ ）
A．小于0.64m3 B．大于0.64m3 C．不小于0.64m3 D．不大于0.64m3
查看答案和解析>>
科目：初中数学 来源： 题型：
.用电脑程序控制小型赛车进行50m比赛，“畅想号”和“和谐号”两赛车进入了决赛，比赛前的练习中，两辆车从起点同时出发，“畅想号”到达终点时，“和谐号”离终点还差3m，已知“畅想号”的平均速度为2.5m/s
（1）求“和谐号”的平均速度;
（2）如果两车重新开始比赛，“畅想号”从起点向后退3m ，两车 同时出发，两车能否同时到达终点？若能，求出两车到达终点的时间;若不能，请重新调整一辆车的平均速度，使两车能同时到达终点。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是AC的中点．若AD=6，DE=5，则CD的长等于 ．