
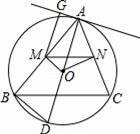
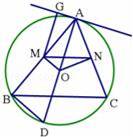
已知:如图,△ABC是⊙O内接三角形,OM⊥AB于点M,ON⊥AC于点N,连接MN,
(1)求证:MN=
 BC;
BC;
(2)过点A作⊙O的直径AD,连接BD,AG为过点A的圆切线,过点M作MG⊥AG,垂足为G,若cos∠BAD=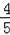
 ,BD=20,求AG的长.
,BD=20,求AG的长.

【考点】切线的性质;勾股定理;三角形中位线定理;垂径定理.
【分析】(1)由垂径定理和三角形的中位线的性质得到结论.
(2)由AD是⊙O的直径,得到∠ABD=90°,解直角三角形得到AD,AB的长度,再由锐角三角函数解出结果.
【解答】(1)证明:∵OM⊥AB于点M,ON⊥AC于点N,
∴点M、N分别是AB、AC的中点,MN是三角形ABC的中位线,
∴MN=
 BC;
BC;
(2)解:∵AD是⊙O的直径,
∴∠ABD=90°,
∵cos∠BAD=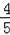
 ,BD=20,
,BD=20,
∴在直角三角形ABD中,可设AD=5k,AB=4K,
根据勾股定理得:(5k)2﹣(4k)2202,
∴k=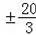
 (﹣
(﹣
 舍去),
舍去),
∴AD=
 ,AB=
,AB=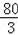
 ,
,
∵AG是⊙O的切线,
∴OA⊥AG,
又∵MG⊥AG,
∴∠GAD=90°=∠MGA,
∴AD∥MG
∴∠AMG=∠BAD
∴sin∠AMG=sin∠BAD=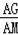
 =
=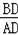
 =
=
 ,
,
∴AG=
 AM=
AM=
 ×
×
 AB=8,
AB=8,
∴AG=8.

【点评】本题考查了三角形的中位线定理,切线的性质,垂径定理,勾股定理,锐角三角函数,掌握垂径定理是解题的关键.


科目:初中数学 来源: 题型:
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
查看答案和解析>>
科目:初中数学 来源: 题型:
四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.
(1)随机抽取一张卡片,求恰好抽到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则如图所示.你认为这个游戏公平吗?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在正方形ABCD中,E是BC边的中点,把△ABE沿直线AE折叠,点B的对应点为B′,AB′的延长线交DC于点F,若FC=2,则正方形的边长为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF交于D,则以下结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.正确的是( )
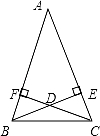
A.① B.② C.①② D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com