练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，⊙O为△ABC的外接圆，∠A=72°，则∠BCO的度数为（　　）

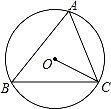
    A．15°   B．18°    C．20°   D．28°

    　


    B【考点】圆周角定理．

    【专题】计算题．

    【分析】连结OB，如图，先根据圆周角定理得到∠BOC=2∠A=144°，然后根据等腰三角形的性质和三角形内角和定理计算∠BCO的度数．

    【解答】解：连结OB，如图，∠BOC=2∠A=2×72°=144°，

    ∵OB=OC，

    ∴∠CBO=∠BCO，

    ∴∠BCO=（180°﹣∠BOC）=×（180°﹣144°）=18°．

    故选B．

    【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等腰三角形的性质．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，AB=AC，BE⊥AC于E，CF⊥AB于F，BE，CF交于D，则以下结论：①△ABE≌△ACF；②△BDF≌△CDE；③点D在∠BAC的平分线上．正确的是（　　）

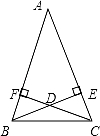
    A．①     B．②     C．①② D．①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：


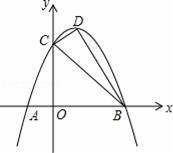
    如图，已知抛物线y=ax2+bx+3交x轴于A、B两点（A在B左边），交y轴于C点，且OC=3OA，对称轴x=1交抛物线于D点．

    （1）求抛物线解析式；

    （2）在直线BC上方的抛物线上找点E使S△BCD=S△BCE，求E点的坐标；

    （3）在x轴上方的抛物线上，是否存在点M，过M作MN⊥x轴于N点，使△BMN与△BCD相似？若存在，请求出M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，△ABC的边BC在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=FP．

    （1）如图1，请你写出AB与AP所满足的数量关系和位置关系（不必证明）；

    （2）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点O，连接AP，BO．猜想并写出BO与AP所满足的数量关系和位置关系，并说明理由；

     
    （3）将△EFP沿直线l继续向左平移到图3的位置时，EP的延长线交AC的延长线于点O，连接AP，BO．此时，BO与AP还具有（2）中的数量关系和位置关系吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，把Rt△ABC绕点A逆时针旋转40°，得到Rt△AB′C′，点C′恰好落在边AB上，连接BB′，则∠BB′C′=　　　　　　度．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    3x（x﹣2）=2（2﹣x）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    反比例函数的图象与一次函数y=2x+1的图象的一个交点是（1，k），则反比例函数的解析式是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为2米，则这个坡面的坡度为（　　）

    A．1：2 B．1：3  C．1：     D．：1

    　

    查看答案和解析>>

    同步练习册答案