
如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)如图1,请你写出AB与AP所满足的数量关系和位置关系(不必证明);
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点O,连接AP,BO.猜想并写出BO与AP所满足的数量关系和位置关系,并说明理由;

| |

 (3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明
(3)将△EFP沿直线l继续向左平移到图3的位置时,EP的延长线交AC的延长线于点O,连接AP,BO.此时,BO与AP还具有(2)中的数量关系和位置关系吗?请说明 理由.
理由. .解:(1)AB=AP;AB⊥AP.
(2)BO=AP;BO⊥AP.
证明:①由已知得:EF=FP,EF⊥FP,
∴∠EPF=45°.
又∵AC⊥BC,∴∠COP=∠CPO=45°.∴CO=CP.
在Rt△BCO和Rt△ACP中,BC=AC,∠BCO=∠ACP=90°,CO=CP,
∴Rt△BCO≌Rt△ACP.∴BO=AP.
②如图,延长BO交AP于点M.
∵Rt△BCO≌Rt△ACP,∴∠OBC=∠PAC.
在Rt△BCO中,∠OBC+∠BOC=90°,又∠BOC=∠AOM,
∴∠PAC+∠AOM=∠OBC+∠BOC=90°.∴∠OMA=90°.∴BO⊥AP.
成立.
证明:①如图,∵∠EPF=45°,∴∠CPO=45°.
又∵AC⊥BC,∴∠COP=∠CPO=45°.∴CO=CP.
在Rt△BCO和Rt△ACP中,
BC=AC,∠BCO=∠ACP=90°,CO=CP,
∴Rt△BCO≌Rt△ACP.∴BO=AP.
|


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
有五张一面分别印有圆、等腰三角形、矩形、菱形、正方形图案的卡片(卡片中除图案不同外,其余均相同),现将有图案的一面朝下任意摆放,从中任意抽取一张,抽到有中心对称图案的卡片的概率是( )
A. B.
B.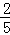 C.
C.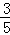 D.
D.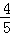
查看答案和解析>>
科目:初中数学 来源: 题型:
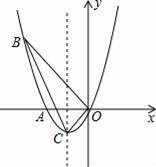
如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com