
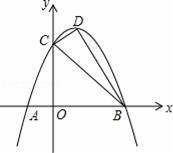
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.

【考点】二次函数综合题.
【分析】(1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(﹣1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而可求得a=﹣1,b=2;
(2)过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点,由△BCD与△BCE是同底等高的三角形可知S△BCD=S△BCE,设直线DE的解析式为y=﹣x+b,将点D的坐标代入可求得直线DE的解析式,然后与抛物线的解析式联立可求得点E的坐标;
(3)由两点间的而距离公式可知:BC=3
 ,CD=
,CD=
 ,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
【解答】解:(1)∵将x=0代入得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1.
∴A(﹣1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(﹣1,0),B(3,0)代入y=ax2+bx+3得: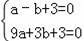
 ,
,
解得:
 .
.
∴抛物线解析式为y=﹣x2+2x+3.
(2)∵将x=1代入抛物线的解析式得:y=﹣1+2+3=4,
∴D(1,4).
如图1,过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点.
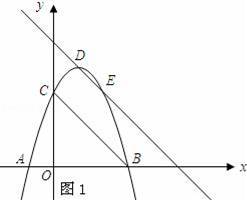

设直线DE的解析式为y=﹣x+b,
将点D的坐标代入得:﹣1+b=4,解得:b=5,则直线DE的解析式为y=﹣x+5.
将y=﹣x+5与y=﹣x2+2x+3联立得: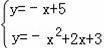
 ,
,
解得: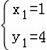
 (舍去),
(舍去),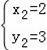
 .
.
∴E(2,3).
(3)存在.
由两点间的而距离公式可知:BC=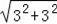
 3
3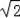
 ,CD=
,CD=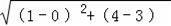
 =
=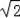
 .
.
设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x.
①如图2所示:
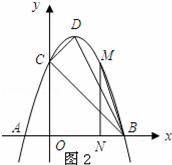

∵当△BMN∽△DBC时,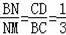
 ,
,
∴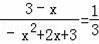
 .
.
解得:x1=2,x2=3(舍去).
∵当x=2时,y=3,
∴M(2,3).
②如图3所示:
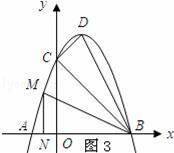

∵当△BMN∽△BDC时,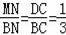
 ,
,
∴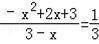
 .
.
解得:x1=﹣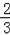
 ,x2=3(舍去).
,x2=3(舍去).
当x=﹣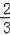
 时,y=
时,y=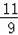
 ,
,
∴M(﹣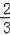
 ,
,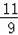
 )
)
综上,存在点M(2,3)或(﹣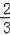
 ,
,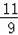
 ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.
【点评】本题主要考查的是二次函数的综合应用,本题主要涉及了待定系数法求一次函数、二次函数的解析式、一次函数与二次函数图象的交点、相似三角形的性质和判定等知识点,依据相似三角形的性质列出关于x的方程是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,⊙O中,AD、BC是圆O的弦,OA⊥BC,∠AOB=50°,CE⊥AD,则∠DCE的度数是( )
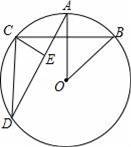

A.25° B.65° C.45° D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列等式:
①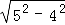 =1×3;②
=1×3;②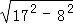 =3×5;③
=3×5;③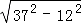 =5×7;
=5×7;
…
根据上述规律解决下列问题:
(1)完成第④个等式: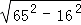 = × ;
= × ;
(2)写出你猜想的第n个等式(用含n的式子表示),并证明其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
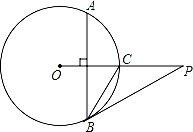
如图,已知点P是⊙O外一点,PO交圆O于点C,OC=2,AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求征:OC=BC;
(2)当PB的长是多少时,PB是⊙O的切线?写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com