
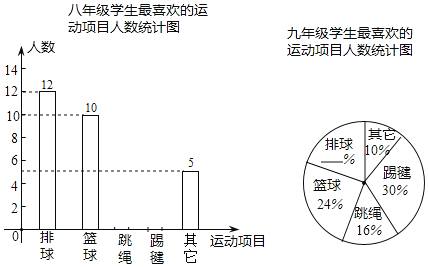
【题目】通辽市某中学为了了解学生“大课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 |
| 6 |
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取了多少人?
(2)补全统计表和统计图.
(3)该校有学生1800人,学校想对“最喜欢踢毽子”的学生每4人提供一个毽子,学校现有124个毽子,能否够用?请说明理由.
【答案】(1)150人;(2)补图见解析;(3)不够用.
【解析】
(1)从九年级最喜欢运动的项目统计图中得知,九年级最喜欢排球的人数占总数的百分数,又知九年级最喜欢排球的人数为10人,所以求出九年级最喜欢运动的人数,再由七、八、九年级的学生中,分别抽取相同数量的学生,得出本次调查共抽取的学生数;
(2)先根据(1)得七年级最喜欢跳绳的人数,从而能求出八、九年级最喜欢跳绳的人数,然后求出最喜欢跳绳的学生数,补全统计表和统计图即可;
(3)根据题意列式计算即可得到结论.
解:(1)从九年级最喜欢运动的项目统计图中得知,九年级最喜欢排球的人数占总数的百分比为:![]() ,
,
又知九年级最喜欢排球的人数为10人,
∴九年级最喜欢运动的人数有![]() (人),
(人),
∴本次调查抽取的学生数为:![]() (人).
(人).
(2)根据(1)得七年级最喜欢跳绳的人数有![]() 人,
人,
那么八年级最喜欢跳绳的人数有![]() 人,
人,
最喜欢踢毽的学生有![]() 人,
人,
九年级最喜欢排球的人数占全年级的百分比=![]()
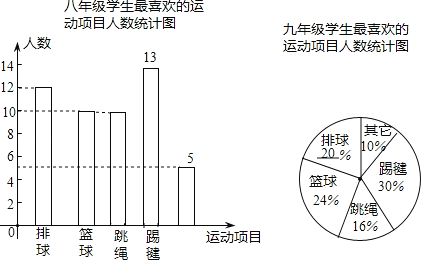
补全统计表和统计图如图所示;
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 15 | 6 |
(3)不够用,理由:![]() ,
,
∵![]() ,
,
∴不够用.
故答案为:15.


科目:初中数学 来源: 题型:
【题目】一驴友分三次从![]() 地出发沿着不同线路(
地出发沿着不同线路(![]() 线、
线、![]() 线、
线、![]() 线)去
线)去![]() 地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;
地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;![]() 线、
线、![]() 线路程相等,都比
线路程相等,都比![]() 线路程多
线路程多![]() ;
;![]() 线总时间等于
线总时间等于![]() 线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完
线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完![]() 线;在
线;在![]() 线中穿越丛林、涉水行走和攀登所用时间分别比
线中穿越丛林、涉水行走和攀登所用时间分别比![]() 线上升了
线上升了![]() .若他用了
.若他用了![]() 小时穿越丛林、
小时穿越丛林、![]() 小时涉水行走和
小时涉水行走和![]() 小时攀登走完
小时攀登走完![]() 线,且
线,且![]() 都为正整数,则
都为正整数,则![]() _____.
_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子1张或椅子4把,现计划用120块这种板材生产一批桌椅(不考虑板材的损耗),设用x块板材做桌子,用y块板材做椅子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人一起步行到火车站,途中发现忘带火车票了,于是甲立刻原速返回,乙继续以原速步行前往火车站,甲取完火车票后乘出租车赶往火车站,途中与乙相遇,带上乙一同前往,结果比预计早到3分钟,他们与公司的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图所示,则下列结论错误的是( )
(分)的函数关系如图所示,则下列结论错误的是( )
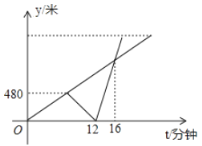
A.他们步行的速度为每分钟80米;B.出租车的速度为每分320米;
C.公司与火车站的距离为1600米;D.出租车与乙相遇时距车站400米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )

A、3或4![]() B、4或3
B、4或3![]() C、3或4 D、3
C、3或4 D、3![]() 或4
或4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)交x轴于A(﹣4,0),B(2,0),在y轴上有一点E(0,﹣2),连接AE.
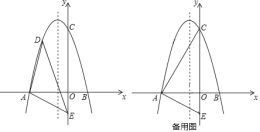
(1)求二次函数的表达式;
(2)点D是第二象限内的抛物线上一动点.
①求△ADE面积最大值并写出此时点D的坐标;
②若tan∠AED=![]() ,求此时点D坐标;
,求此时点D坐标;
(3)连接AC,点P是线段CA上的动点,连接OP,把线段PO绕着点P顺时针旋转90°至PQ,点Q是点O的对应点.当动点P从点C运动到点A,则动点Q所经过的路径长等于 (直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com