
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.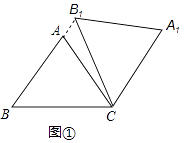
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.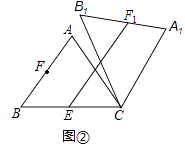
【答案】
(1)①证明:∵AB=AC,B1C=BC,
∴∠BB1C=∠B,∠B=∠ACB,
∵∠A1CB1=∠ACB(旋转角相等),
∴∠BB1C=∠A1CB1,
∴BB1∥CA1,
②过A作AF⊥BC于F,过C作CE⊥AB于E,

∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC=0.6,AB=5,
∴BF=3,
∴BC=6∴B1C=BC=6
∵CE⊥AB,
∴BE=B1E= ![]() ×6=
×6= ![]() ,
,
∴BB1= ![]() ,CE=
,CE= ![]() ,
,
∴AB1= ![]() ,
,
∴△AB1C的面积为: ![]() =
= ![]()
(2)解:如图3,
过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值.
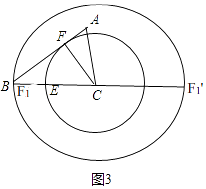
此时在Rt△BFC中,CF=4.8,
∴CF1=4.8,
∴EF1的最小值为4.8﹣3=1.8;
如图,以C为圆心BC为半径画圆交BC的延长线于F1',EF1'有最大值.
此时EF1'的最大值为EC+CF1'=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣1.8=7.2.
【解析】(1)①根据旋转的性质和平行线的性质可证得BB1∥CA1;②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质、解直角三角形及三角形的面积公式,即可求得答案。
(2)此题转化到圆中求解,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,可求得EF1的最小值,以C为圆心BC为半径画圆交BC的延长线于F1',求得EF1'的最大值,即可求得线段EF1的最大值与最小值的差。


科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABD中,∠A=90°,AB=AD=2,作△ABD关于直线BD对称的△CBD,已知点F为线段AB上一点,且AF=m,连接CF,作∠FCE=90°,CE交AD的延长线于点E.
(1)求证:△BCF≌△DCE;
(2)若AE=n,且mn=3,求m2+n2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图:在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形.按要求画出下列图形:
(1)将△ABC向右平移5个单位得到△A′B′C′;
(2)将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;
(3)连结EC′,则△A′EC′是 三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC绕点A逆时针方向旋转得到△ADE,其中∠B=50°,∠C=60°.
(1)若AD平分∠BAC时,求∠BAD的度数.
(2)若AC⊥DE时,AC与DE交于点F,求旋转角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题
王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44000元.其中种茄子每亩用了1700元,获纯利2400元;种西红柿每亩用了1800元,获纯利2600元.
问(1)茄子和西红柿各种了多少亩?
(2)王大伯一共获纯利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com