
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
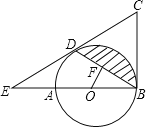
(1)求证:CD为⊙O的切线;
(2)若OF⊥BD于点F,且OF=2,BD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)见解析;(2)S阴影=![]() .
.
【解析】
(1)首先连接OD,由BC是⊙O的切线,可得∠ABC=90°,又由CD=CB,OB=OD,易证得∠ODC=∠ABC=90°,即可证得CD为⊙O的切线;
(2)在Rt△OBF中,求出∠ABD=30°,得出∠BOD的度数,又由S阴影=S扇形OBD-S△BOD,即可求得答案.
(1)证明:连接OD,如图所示:
∵BC是⊙O的切线,
∴∠ABC=90°,
∵CD=CB,
∴∠CBD=∠CDB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODC=∠ABC=90°,
即OD⊥CD,
∵点D在⊙O上,
∴CD为⊙O的切线;
(2)解:∵OF⊥BD,
∴BF=![]() BD=2
BD=2![]() ,OB=
,OB=![]() =
=![]() =4,
=4,
∴OF=![]() OB,
OB,
∴∠OBF=30°,
∴∠BOF=60°,
∴∠BOD=2∠BOF=120°,
∴S阴影=S扇形OBD﹣S△BOD=![]() ﹣
﹣![]() ×4
×4![]() ×2=
×2=![]() ﹣4
﹣4![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
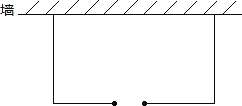
【题目】如图,要建一个底面积为130平方米的仓库,仓库一边靠墙(墙长16米),并在与墙平行的一边开道1米宽的门,现有能围成32米长的木板.请你设计如何搭建比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
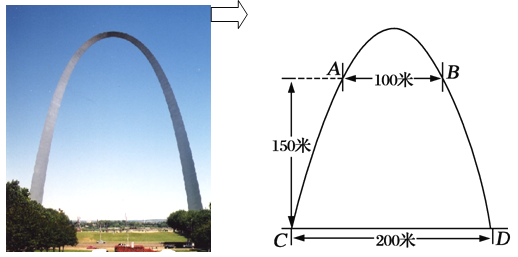
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色的正方形瓷砖铺设长方形地面,观察下列图形并解答问题.
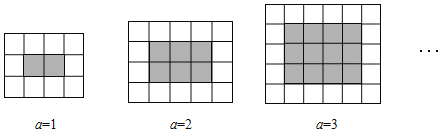
(1)在第a个图中,共有 块白瓷砖和 块黑瓷砖(用含a的代数式表示);
(2)若按上图的方式铺一块长方形地面共用了420块瓷砖,求此时a的值;
(3)已知白瓷砖每块6元,黑瓷砖每块8元,某工厂按如图方式铺设厂房地面,其中黑瓷砖的费用比白瓷砖的费用多924元,问白瓷砖和黑瓷砖各用了多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,5)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是______________.
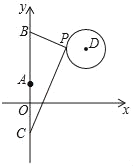
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(3,0)、B(1,0),与y轴交于点C(0,3)。
与x轴交于A(3,0)、B(1,0),与y轴交于点C(0,3)。
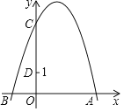
(1)求抛物线![]() 的解析式;
的解析式;
(2)若点D(0,1),点P是抛物线上的动点,且△PCD是以CD为底的等腰三角形,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com