
【题目】如图,![]()
![]() 中,
中,![]() 的顶点
的顶点![]() 分别在
分别在![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 随之在边
随之在边![]() 上运动,
上运动,![]() 的形状保持不变,在运动过程中,点
的形状保持不变,在运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )
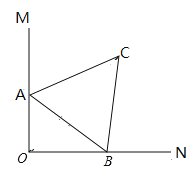
A.7B.5C.4D.3
【答案】A
【解析】
取AB的中点D,连接CD,根据三角形的边角关系得到OC≤OD+DC,只有当O、D及C共线时,OC取得最大值,最大值为OD+CD,根据D为AB中点,得到BD=3,根据三线合一得到CD垂直于AB,在Rt△BCD中,根据勾股定理求出CD的长,在Rt△AOB中,OD为斜边AB上的中线,根据直角三角形斜边上的中线等于斜边的一半可得OD的值,进而求出DC+OD,即为OC的最大值.
取AB的中点D,连接CD,
∵AC=BC=5,AB=6,
∵点D是AB边中点,
∴BD=![]() AB=3,CD⊥AB,
AB=3,CD⊥AB,
∴CD=![]() ,
,
连接OD,OC,有OC≤OD+DC,
当O、D.、C共线时,OC有最大值,最大值=OD+CD,
∵△AOB为直角三角形,D为斜边AB的中点,
∴OD=![]() AB=3,
AB=3,
∴OD+CD=3+4=7,即OC的最大值=7.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+4x+c的图象与x轴交于A、B两点,与y轴交于点C,其中A(﹣1,0),C(0,5)
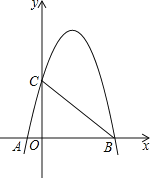
(1)求二次函数的解析式,并求出当x=1时的函数值.
(2)连接BC,AC,得到△ABC,现将抛物线图象只向下平移m个单位,使得顶点落在△ABC内部(不包括边界),请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
观察下列方程:①![]() ;②
;②![]() ;③
;③![]() ;…;
;…;
(1)按此规律写出关于x的第4个方程为 ,第n个方程为 ;
(2)直接写出第n个方程的解,并检验此解是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字2、3、4、6的乒乓球,它们的形状、大小、颜色、质地完全相同,耀华同学先从盒子里随机取出一个小球,记为数字x,不放回,再由洁玲同学随机取出另一个小球,记为数字y,
(1)用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;
(2)求取出的坐标(x,y)对应的点落在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的图柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() .敏敏观察到高度
.敏敏观察到高度![]() 矮圆柱的影子落在地面上,其影长为
矮圆柱的影子落在地面上,其影长为![]() ;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
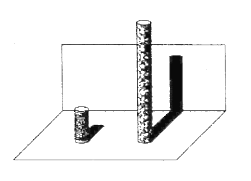
(1)若敏敏的身高为![]() ,且此刻她的影子完全落在地面上,求影子的长度.
,且此刻她的影子完全落在地面上,求影子的长度.
(2)若同一时间量得高圆柱落在墙上的影长为![]() ,请你画出示意图并求出高圆柱的高度.
,请你画出示意图并求出高圆柱的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
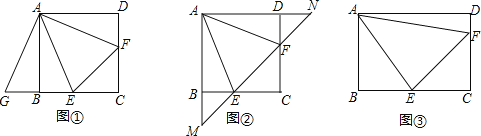
【题目】正方形![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)将![]() 绕着点
绕着点![]() 顺时针旋转90°,得到
顺时针旋转90°,得到![]() (如图①),求证:
(如图①),求证:![]() ;
;
(2)若直线![]() 与
与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() (如图②),求证:
(如图②),求证:![]() ;
;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系 .(不要求书写证明过程)
之间的数量关系 .(不要求书写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
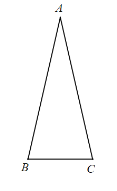
【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com