
【题目】阅读材料,解答问题:
观察下列方程:①![]() ;②
;②![]() ;③
;③![]() ;…;
;…;
(1)按此规律写出关于x的第4个方程为 ,第n个方程为 ;
(2)直接写出第n个方程的解,并检验此解是否正确.
【答案】(1)9,2n+1;(2)2n+1,见解析
【解析】
(1)观察一系列等式左边分子为连续两个整数的积,右边为从3开始的连续奇数,即可写出第4个方程及第n个方程;
(2)归纳总结即可得到第n个方程的解为n与n+1,代入检验即可.
解:(1)x+![]() =x+
=x+![]() =9,x+
=9,x+![]() =2n+1;
=2n+1;
故答案为:x+![]() =9;x+
=9;x+![]() =2n+1.
=2n+1.
(2)x+![]() =2n+1,
=2n+1,
观察得:x1=n,x2=n+1,
将x=n代入方程左边得:n+n+1=2n+1;右边为2n+1,
左边=右边,即x=n是方程的解;
将n+1代入方程左边得:n+1+n=2n+1;右边为2n+1,
左边=右边,即x=n+1是方程的解,
则经检验都为原分式方程的解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园划船项目收费标准如下:某班18名同学一起去该公园划船,若每人划船的时间均为1小时,则租船的总费用最低为_____元.
船型 | 两人船(限乘两 人) | 四人船(限乘四 人) | 六人船(限乘六 人) | 八人船(限乘八 人) |
每船租金(元/小时) | 50 | 80 | 100 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:
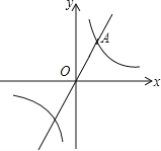
【题目】 如图,已知正比例函数y=kx与反比例函数y=![]() 的图象在第一象限交于点A(2,4).
的图象在第一象限交于点A(2,4).
(1)求正比例函数与反比例函数的解析式.
(2)平移直线OA,平移后的直线与x轴交于点B,与反比例函数的图象交于第一象限的点C(4,n).
①求直线BC的解析式;
②线段BC的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了每个营业员在某月的销售额,绘制了如下统计图.
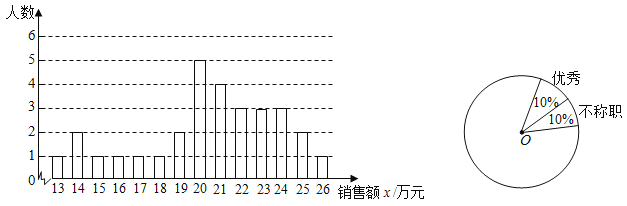
解答下列问题:
(1)设营业员的月销售额为x(单位:万元).商场规定:当x<15时为不称职,当15≤x<20时为基本称职,当20≤x<25时为称职,当x≥25时为优秀.试求出基本称职、称职两个层次营业员人数所占百分比,并补全扇形图;
(2)根据(1)中规定,所有称职和优秀的营业员月销售额的中位数为 ,众数为 ;
(3)为了调动营业员的积极性,商场制定月销售额奖励标准,凡达到或超过这个标准的受到奖励.如果要使称职和优秀的营业员半数左右能获奖,奖励标准应定为多少万元?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
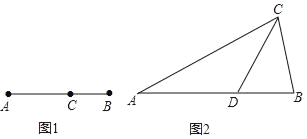
【题目】如图1,我们已经学过:点C将线段AB分成两部分,如果![]() ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D.
(1)证明点D是AB边上的黄金分割点;
(2)证明直线CD是△ABC的黄金分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为0或4时,函数值都为-3,当自变量
的值为0或4时,函数值都为-3,当自变量![]() 的值为-1或5时,函数值为2.
的值为-1或5时,函数值为2.
探究过程如下,请补充完整.
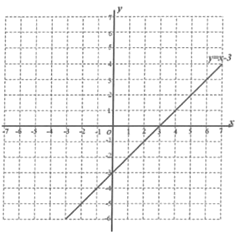
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有4个解,则k的取值范围为 ;
有4个解,则k的取值范围为 ;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]()
![]() 中,
中,![]() 的顶点
的顶点![]() 分别在
分别在![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 随之在边
随之在边![]() 上运动,
上运动,![]() 的形状保持不变,在运动过程中,点
的形状保持不变,在运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )
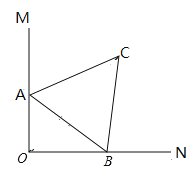
A.7B.5C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm,中轴轴心C到地面的距离CF为30cm,座位高度最低刻度为155cm,此时车架中立管BC长为54cm,且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)
(1)求车座B到地面的高度(结果精确到1cm);
(2)根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)
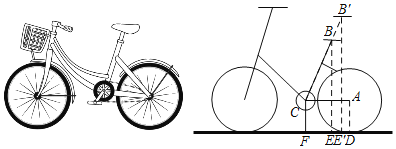
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com