
【题目】在公园有两座垂直于水平地面且高度不一的图柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() .敏敏观察到高度
.敏敏观察到高度![]() 矮圆柱的影子落在地面上,其影长为
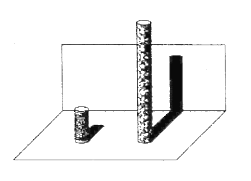
矮圆柱的影子落在地面上,其影长为![]() ;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() ,且此刻她的影子完全落在地面上,求影子的长度.
,且此刻她的影子完全落在地面上,求影子的长度.
(2)若同一时间量得高圆柱落在墙上的影长为![]() ,请你画出示意图并求出高圆柱的高度.
,请你画出示意图并求出高圆柱的高度.
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价3元,当天可获利多少元?
(2)设每件商品降价x元,在销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?
(3)当降价多少时,商场可获得最大利润?(取下降价格为整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
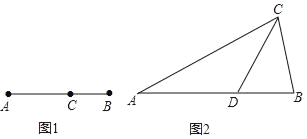
【题目】如图1,我们已经学过:点C将线段AB分成两部分,如果![]() ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D.
(1)证明点D是AB边上的黄金分割点;
(2)证明直线CD是△ABC的黄金分割线.
查看答案和解析>>
科目:初中数学 来源: 题型:
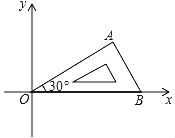
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]()
![]() 中,
中,![]() 的顶点
的顶点![]() 分别在
分别在![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 随之在边
随之在边![]() 上运动,
上运动,![]() 的形状保持不变,在运动过程中,点
的形状保持不变,在运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )
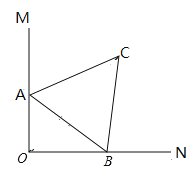
A.7B.5C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
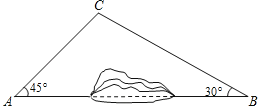
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶,已知BC=80千米,∠A=45°,∠B=30°,
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到1千米)(参考数据:![]() =1.4,
=1.4,![]() =1.7)
=1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
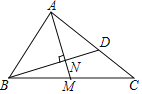
【题目】已知:如图,在△ABC中,∠BAC=90°,M是斜边BC的中点,BN⊥AM,垂足为点N,且BN的延长线交AC于点D.
(1)求证:△ABC∽△ADB;
(2)如果BC=20,BD=15,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
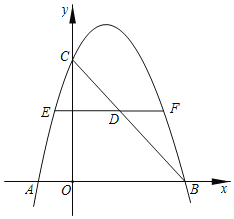
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
(1)求抛物线的对称轴和函数表达式.
(2)连结BC线段,BC上有一点D,过点D作x轴的平行线交抛物线于点E,F,若EF=6,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
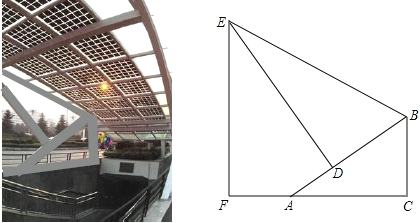
【题目】如图是某地下商业街的入口,数学课外兴趣小组同学打算运用所学知识测量侧面支架最高点E到地面距离EF.经测量,支架立柱BC与地面垂直,即∠BCA=90°,且BC=1.5cm,点F、A、C在同一条水平线上,斜杆AB与水平线AC夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架边BE与AB夹角∠EBD=60°,又测得AD=1m.请你求出该支架边BE及顶端E到地面距离EF长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com