
【题目】商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价3元,当天可获利多少元?
(2)设每件商品降价x元,在销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?
(3)当降价多少时,商场可获得最大利润?(取下降价格为整数)
【答案】(1)若某天该商品每件降价3元,当天可获利1692元;(2)每件商品降价25元时,商场日盈利可达到2000元;(3)17元或18元
【解析】
(1)根据“盈利=单件利润×销售数量”即可得出结论;
(2)根据“盈利=单件利润×销售数量”即可列出关于x的一元二次方程,解之即可得出x的值,再根据尽快减少库存即可确定x的值.
(3)设降价m元时可获得利润y,则y=(50-m)×(30+2m),再将其化简即可求解.
解:(1)当天盈利:(50﹣3)×(30+2×3)=1692(元).
答:若某天该商品每件降价3元,当天可获利1692元.
(2)根据题意,得:(50﹣x)×(30+2x)=2000,
整理,得:x2﹣35x+250=0,
解得:x1=10,x2=25,
∵商城要尽快减少库存,
∴x=25.
答:每件商品降价25元时,商场日盈利可达到2000元.
(3)设降价m元时可获得利润y ,
则y=(50-m)×(30+2m)![]()

∴当x=17.5时,W取得最大值,最大值为2112.5,
∵取下降价格为整数,
则m的为17元或18元


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.

(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+4x+c的图象与x轴交于A、B两点,与y轴交于点C,其中A(﹣1,0),C(0,5)
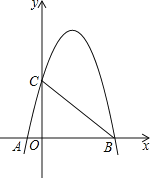
(1)求二次函数的解析式,并求出当x=1时的函数值.
(2)连接BC,AC,得到△ABC,现将抛物线图象只向下平移m个单位,使得顶点落在△ABC内部(不包括边界),请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则雪道AB的长度为( )

A.200 米B.(200+200![]() )米
)米
C.600 米D.(200+20![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB.

(1)求证:AC是⊙O的切线;
(2)若cosC=![]() ,AC=6,求BF的长.
,AC=6,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.概率是1%的事件在一次试验中一定不会发生
B.要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式
C.甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定
D.随意翻到一本书的某页,页码是奇数是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
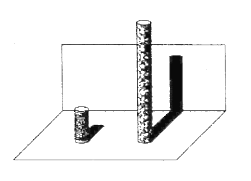
【题目】在公园有两座垂直于水平地面且高度不一的图柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() .敏敏观察到高度
.敏敏观察到高度![]() 矮圆柱的影子落在地面上,其影长为
矮圆柱的影子落在地面上,其影长为![]() ;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
(1)若敏敏的身高为![]() ,且此刻她的影子完全落在地面上,求影子的长度.
,且此刻她的影子完全落在地面上,求影子的长度.
(2)若同一时间量得高圆柱落在墙上的影长为![]() ,请你画出示意图并求出高圆柱的高度.
,请你画出示意图并求出高圆柱的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com