
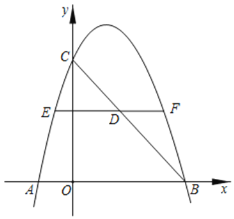
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
x2+2x+a交x轴于点A,B,交y轴于点C,点A的横坐标为﹣2.
(1)求抛物线的对称轴和函数表达式.
(2)连结BC线段,BC上有一点D,过点D作x轴的平行线交抛物线于点E,F,若EF=6,求点D的坐标.
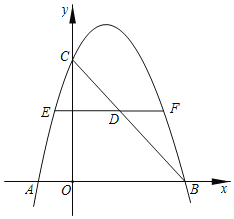
【答案】(1)y=﹣![]() x2+2x+6;对称轴为x=2;(2)点D的坐标为(2.5,1.5).
x2+2x+6;对称轴为x=2;(2)点D的坐标为(2.5,1.5).
【解析】
(1)将点A的坐标代入函数的解析式求得a的值后即可确定二次的解析式,代入对称轴公式即可求得对称轴;
(2)首先根据点A的坐标和对称轴求得点B的坐标,然后求得直线BC的解析式,从而设出点D的坐标并表示出点EF的坐标,表示出EF的长后根据EF=6求解即可.
解:如图:
(1)∵A点的横坐标为﹣2,
∴A(﹣2,0),
∵点A 在抛物线y=﹣![]() x2+2x+a上,
x2+2x+a上,
∴﹣2﹣4+a=0,
解得:a=6,
∴函数的解析式为:y=﹣![]() x2+2x+6,
x2+2x+6,
∴对称轴为x=﹣![]() =﹣
=﹣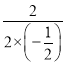 =2;
=2;
(2)∵A(﹣2,0),对称轴为x=2,
∴点B的坐标为(6,0),
∴直线BC的解析式为y=﹣x+6,
∵点D在BC上,
∴设点D的坐标为(m,﹣m+6),
∴点E和点F的纵坐标为﹣m+6,
∴y=﹣![]() x2+2x+6=﹣m+6,
x2+2x+6=﹣m+6,
解得:x=2±![]() ,
,
∴EF=2+![]() ﹣(2﹣
﹣(2﹣![]() )=2
)=2![]() ,
,
∵EF=6,
∴2![]() =6,
=6,
解得:m=2.5,
∴点D的坐标为(2.5,1.5).


科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.概率是1%的事件在一次试验中一定不会发生
B.要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式
C.甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定
D.随意翻到一本书的某页,页码是奇数是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在公园有两座垂直于水平地面且高度不一的图柱,两座圆柱后面有一堵与地面互相垂直的墙,且圆柱与墙的距离皆为![]() .敏敏观察到高度
.敏敏观察到高度![]() 矮圆柱的影子落在地面上,其影长为
矮圆柱的影子落在地面上,其影长为![]() ;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
;而高圆柱的部分影子落在墙上,如图所示.已知落在地面上的影子皆与墙面互相重直,并视太阳光为平行光,在不计圆柱厚度与影子宽度的情况下,请回答下列问题:
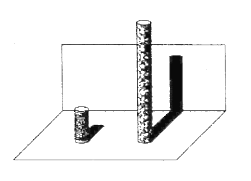
(1)若敏敏的身高为![]() ,且此刻她的影子完全落在地面上,求影子的长度.
,且此刻她的影子完全落在地面上,求影子的长度.
(2)若同一时间量得高圆柱落在墙上的影长为![]() ,请你画出示意图并求出高圆柱的高度.
,请你画出示意图并求出高圆柱的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
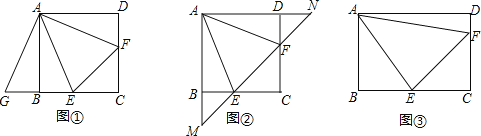
【题目】正方形![]() 中,点
中,点![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() .
.
(1)将![]() 绕着点
绕着点![]() 顺时针旋转90°,得到
顺时针旋转90°,得到![]() (如图①),求证:
(如图①),求证:![]() ;
;
(2)若直线![]() 与
与![]() ,
,![]() 的延长线分别交于点
的延长线分别交于点![]() (如图②),求证:
(如图②),求证:![]() ;
;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系 .(不要求书写证明过程)
之间的数量关系 .(不要求书写证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
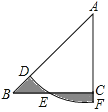
【题目】如图.在Rt△ABC中,∠ACB=90°,AC=BC,以A为圆心,AD长为半径的弧DF交AC的延长线于F,若图中两个阴影部分的面积相等,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:有一角重合,且角的两边叠合在一起的两个相似四边形叫做“嵌套四边形”,如图,四边形ABCD和AMPN就是嵌套四边形.
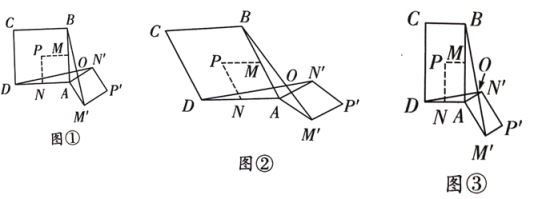
(1)问题联想
如图①,嵌套四边形ABCD,AMPN都是正方形,现把正方形AMPN以A为中心顺时针旋转150°得到正方形AM'P'N',连接BM',DN'交于点O,则BM'与DN'的数量关系为_____,位置关系为_____;
(2)类比探究
如图②,将(1)中的正方形换成菱形,∠BAD=∠MAN=60,其他条件不变,则(1)中的结论还成立吗? 若成立,请说明理由;若不成立,请给出正确的结论,并说明理由;
(3)拓展延伸
如图3,将(1)中的嵌套四边形ABCD和AMPN换成是长和宽之比为2:1的矩形,旋转角换成α(90°<α<180°),其他条件不变,请直接写出BM'与DN'的数量关系和位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=mx2+(5m+3)x+4m(m为常数且m≠0)有以下三种说法:
①不论m为何值,函数图象一定过定点(﹣1,﹣3);
②当m=﹣1时,函数图象与坐标轴有3个交点;
③当m<0,x≥﹣![]() 时,函数y随x的增大而减小;判断真假,并说明理由.
时,函数y随x的增大而减小;判断真假,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com