Question

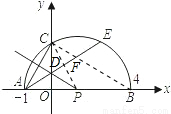
如图所示，已知两点A（-1，0），B（4，0），以AB为直径的半圆P交y轴于点C．

（1）求经过A、B、C三点的抛物线的解析式；

（2）设弦AC的垂直平分线交OC于D，连接AD并延长交半圆P于点E，与相等吗？请证明你的结论；

（3）设点M为x轴负半轴上一点，OM=AE，是否存在过点M的直线，使该直线与（1）中所得的抛物线的两个交点到y轴的距离相等？若存在，求出这条直线对应函数的解析式；若不存在．请说明理由．

 

 

Answer 1

（1）；

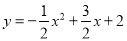（2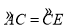），证明见解析；

（3）不存在，理由见解析．

【解析】

试题分析：（1）本题的关键是求出C点的坐标，可通过构建直角三角形来求解．连接BC，即可根据射影定理求出OC的长，也就得出了C点的坐标，已知了A，B，C三点的坐标后即可用待定系数法求出抛物线的解析式．

（2）求弧AC=弧CE，可通过弧对的圆周角相等来证，即证∠EAC=∠ABC，根据等角的余角相等不难得出∠ACO=∠ABC，因此只需证∠DCA=∠DAC即可．由于PD是AC的垂直平分线，根据线段垂直平分线上的点到线段两端点的距离相等，可得出DA=DC，即可证得∠DAC=∠DCA，由此可证出弧AC=弧CE．

（3）可先求出M点的坐标，由于OM=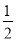AE，因此要先求出AE的长．如果连接PC，设PC与AE的交点为F，那么OF=OM=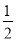AE，OF的长可通过证三角形CAO和AFC全等来得出，有了OM的长就能得出M的坐标．可先设出过M于抛物线相交的直线的解析式．然后根据两交点到y轴的距离相等，即横坐标互为相反数，可根据（1）的抛物线的解析式表示出着两个交点的坐标，然后将两交点和M的坐标代入直线的解析式中，可得出一个方程组，如果方程组无解，那么不存在这样的直线，如果有解，可根据方程组的解得出直线的解析式．

（1）如图，连接BC，

∵AB为直径，

∴∠ACB=90度．

∴OC2=OA•OB，

∵A（-1，0），B（4，0），

∴OA=1，OB=4，

∴OC2=4，

∴OC=2，

∴C的坐标是（0，2）．

设经过A、B、C三点的抛物线的解析式为y=a（x+1）（x-4），

把x=0时，y=2代入上式得：

a=-，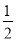

∴．

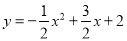（2）．

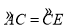证明：∵∠ACB=90度．

∴∠CAB+∠ABC=90度．

∵∠CAB+∠ACO=90度．

∴∠ABC=∠ACO．

∵PD是AC的垂直平分线，

∴DA=DC，

∴∠EAC=∠ACO．

∴∠EAC=∠ABC，

∴．

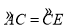（3）不存在．

如图，连接PC交AE于点F，

∵，

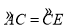∴PC⊥AE，AF=EF，

∵∠EAC=∠ACO，∠AFC=∠AOC=90°，

AC=CA，

∴△ACO≌△CAF，

∴AF=CO=2，

∴AE=4．

∵OM=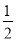AE，

∴OM=2．

∴M（-2，0），

假设存在，设经过M（-2，0）和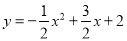相交的直线是y=kx+b；

因为交点到y轴的距离相等，所以应该是横坐标互为相反数，

设两横坐标分别是a和-a，则两个交点分别是（a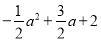，）与（-a，），

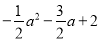把以上三点代入y=kx+b，得

，

此方程无解，所以不存在这样的直线．

考点：二次函数综合题．