
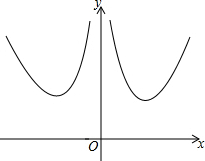
 函数y=x2+$\frac{4}{{x}^{2}}$的图象如图所示,关于该函数下列结论正确的是①②③(填序号).
函数y=x2+$\frac{4}{{x}^{2}}$的图象如图所示,关于该函数下列结论正确的是①②③(填序号).分析 ①把x=-2代入y=x2+$\frac{4}{{x}^{2}}$可得函数图象经过点(-2,5),故①正确;
②根据函数图象有最低点,可得函数有最小值,故②正确;
③解方程可得有4个解,故③正确;
④解出等式x2+$\frac{4}{{x}^{2}}$≤5的解集是-2≤x≤-1或1≤x≤2,于是判断故④错误,
解答 解:①当x=-2时,y=(-2)2$+\frac{4}{(-2)^{2}}$=5,
∴函数图象经过点(-2,5),故①正确;
②∵由图象知:函数图象有最低点,
∴函数可取得最小值,故②正确;
③解方程x2+$\frac{4}{{x}^{2}}$=5得:x=±1,x=±2,
∴方程x2+$\frac{4}{{x}^{2}}$=5有4个解,故③正确;
④等式x2+$\frac{4}{{x}^{2}}$≤5的解集为:-2≤x≤-1或1≤x≤2,
故④错误,
故答案为:①②③.
点评 本题考查了二次函数与不等式,二次函数的图象和最值,正确的识别图象是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4,$\frac{OD}{BD}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
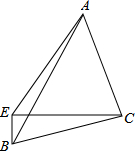 如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.
如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com