
 ��ͼ��һ�κ���y=kx+2��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ڵ�P����P�ڵ�һ���ޣ�PA��x���ڵ�A��PB��y���ڵ�B��һ�κ�����ͼ��ֱ�x�ᡢy���ڵ�C��D����S��PBD=4��$\frac{OD}{BD}$=$\frac{1}{2}$��
��ͼ��һ�κ���y=kx+2��ͼ���뷴��������y=$\frac{m}{x}$��ͼ���ڵ�P����P�ڵ�һ���ޣ�PA��x���ڵ�A��PB��y���ڵ�B��һ�κ�����ͼ��ֱ�x�ᡢy���ڵ�C��D����S��PBD=4��$\frac{OD}{BD}$=$\frac{1}{2}$������ ��1����BP��OA��Rt��PBD��Rt��DOC����$\frac{OD}{BD}$=$\frac{1}{2}$���ɵ�$\frac{OC}{PB}$=$\frac{OD}{BD}$=$\frac{1}{2}$����BD=4��AP=4+2=6����S��PBD=4�ɵ�BP=2����P��2��6���ֱ����y=kx+2��y=$\frac{m}{x}$�ɵ�һ�κ�������ʽΪ��y=2x+2��������������ʽΪ��y=$\frac{12}{x}$��
��2����Rt��PBD�У����PD=$\sqrt{B{D}^{2}+P{B}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$���ٵ���M��x����ʱ����M��m��0������PD=DM=2$\sqrt{5}$��PM=DMʱ�ֱ���ý�����ڵ���M��y����ʱ����M��0��m������PD=PM=2$\sqrt{5}$����PD=DM=2$\sqrt{5}$�ֱ���ý����
��� �⣺��1����BP��OA��
���CDO=��PDB����COD=��CAP��
��Rt��PBD��Rt��DOC��
��$\frac{OD}{BD}$=$\frac{1}{2}$��OD=2��
��BD=4��
��AP=6��
����S��PBD=$\frac{1}{2}$BP•BD=4���ɵ�BP=2��
��P��2��6����P��2��6���ֱ����y=kx+2��y=$\frac{m}{x}$�ɵ�
һ�κ�������ʽΪ��y=2x+2��
��������������ʽΪ��y=$\frac{12}{x}$��
��2����Rt��PBD��PD=$\sqrt{B{D}^{2}+P{B}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��
�ɡ�PDMΪ���������Σ�
�ٵ���M��x����ʱ����M��m��0����
��PD=DM=2$\sqrt{5}$��
��m2+22=��2$\sqrt{5}$��2����ã�m=��4��
��M��-4��0������4��0����
��PM=DM��
��PA2+MA2=OD2+OM2
��62+��m-2��2=22+m2����ã�m=9��
��M��9��0����
�ڵ���M��y����ʱ����M��0��m����
��PD=PM=2$\sqrt{5}$����BM=BD=4��
��M��0��10����
��PD=DM=2$\sqrt{5}$����OM=2+2$\sqrt{5}$����OM=2-2$\sqrt{5}$��
��M��0��2+2$\sqrt{5}$������0��2-2$\sqrt{5}$����
������������ʹ��PDM��Ϊ���������εĵ�M������Ϊ����-4��0������4��0������9��0������0��10������0��2+2$\sqrt{5}$������0��2-2$\sqrt{5}$����
���� ���⿼���˷�����������һ�κ�������ʽ��ȷ����ͼ�ε���������������ε��ж������ʣ�ע���������˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
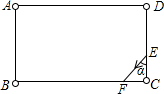 ��ͼ������̨����ABCD������A��B��C��D��������֪DE=4��CE=2��BC=6$\sqrt{3}$�����E���������DC�н�Ϊ��������BC��AB��AD���η�����ص�E�㣬��tan����ȡֵ��Χ��������
��ͼ������̨����ABCD������A��B��C��D��������֪DE=4��CE=2��BC=6$\sqrt{3}$�����E���������DC�н�Ϊ��������BC��AB��AD���η�����ص�E�㣬��tan����ȡֵ��Χ��������| A�� | $\sqrt{3}$��tan����$\frac{3}{2}$$\sqrt{3}$ | B�� | $\frac{3\sqrt{3}}{4}$��tan����$\frac{3}{2}$$\sqrt{3}$ | C�� | tan��=$\sqrt{3}$ | D�� | $\frac{3\sqrt{3}}{4}$��tan����3$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
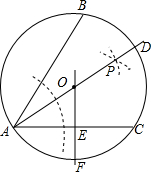 ��ͼ����A��B��C��һ����֪Բ�ϣ�ͨ��һ�������ij߹���ͼ����������AP����֪Բ�ڵ�D��ֱ��OF��ֱƽ��AC����AD�ڵ�O����AC�ڵ�E������֪Բ�ڵ�F��
��ͼ����A��B��C��һ����֪Բ�ϣ�ͨ��һ�������ij߹���ͼ����������AP����֪Բ�ڵ�D��ֱ��OF��ֱƽ��AC����AD�ڵ�O����AC�ڵ�E������֪Բ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
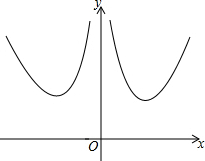 ����y=x2+$\frac{4}{{x}^{2}}$��ͼ����ͼ��ʾ�����ڸú������н�����ȷ���Ǣ٢ڢۣ�����ţ���
����y=x2+$\frac{4}{{x}^{2}}$��ͼ����ͼ��ʾ�����ڸú������н�����ȷ���Ǣ٢ڢۣ�����ţ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
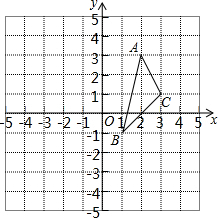 ��ƽ��ֱ������ϵxOy�У���ABC��λ����ͼ��ʾ���Ȱѡ�ABC��x�ᷭ�ۣ��ٰ����õ�ͼ����y�ᷭ�ۣ��õ���A1B1C1
��ƽ��ֱ������ϵxOy�У���ABC��λ����ͼ��ʾ���Ȱѡ�ABC��x�ᷭ�ۣ��ٰ����õ�ͼ����y�ᷭ�ۣ��õ���A1B1C1�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
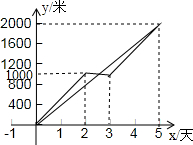 �ڳ����С��������ݡ����̽�������У�ij·�γ�4000�ף��ɼס����������̶Ӻ�����ɣ����̶��ڽ���2�����Ϣ��һ��ʱ�䣬������ԭ�����ٶȽ��裮�ҹ��̶�һֱ���н��裬�����̶�ֱ�������һ·�εĽ���ֹͣ��������ס��ҹ��̶ӽ����·�γ��ȷֱ�Ϊy�����ף���y�����ף��������ʱ��Ϊx���죩��y�ף�y����x֮��ĺ���ͼ����ͼ��ʾ�����ͼ�����������⣺
�ڳ����С��������ݡ����̽�������У�ij·�γ�4000�ף��ɼס����������̶Ӻ�����ɣ����̶��ڽ���2�����Ϣ��һ��ʱ�䣬������ԭ�����ٶȽ��裮�ҹ��̶�һֱ���н��裬�����̶�ֱ�������һ·�εĽ���ֹͣ��������ס��ҹ��̶ӽ����·�γ��ȷֱ�Ϊy�����ף���y�����ף��������ʱ��Ϊx���죩��y�ף�y����x֮��ĺ���ͼ����ͼ��ʾ�����ͼ�����������⣺�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com