
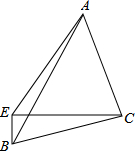
 如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$.
如图,△ABC中,AC=BC,∠BCA=90°,E为△ABC外一点,连结AE、BE、CE,若∠BEC=90°,AE=$\sqrt{13}$BE,则tan∠BCE=$\frac{1}{3}$. 分析 过点A作AF⊥EC,垂足为F,先证明△AFC≌△CEB,从而可证明FC=BE,AF=EC,设ED=x,EC=y,则FC=x,AF=y,FE=y-x,AE=$\sqrt{13}$x,在Rt△AEF中,由勾股定理得:AE2=EF2+AF2,即$(\sqrt{13}x)^{2}=(y-x)^{2}+{y}^{2}$,从而可求得$\frac{x}{y}=\frac{1}{3}$,从而可求得tan∠BCE的值.
解答 解:过点A作AF⊥EC,垂足为F.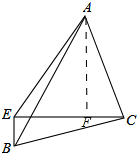
∵AF⊥EC,∠BEC=90°,
∴∠BEC=∠AFC.
∵∠EBC+∠BCE=90°,∠BCE+∠FCA=90°,
∴∠BCE=∠FCA
在△AFC和△CEB中,
$\left\{\begin{array}{l}{∠BEC=∠AFC}\\{∠BCE=∠FCA}\\{AC=BC}\end{array}\right.$.
∴△AFC≌△CEB.
∴FC=BE,AF=EC.
设ED=x,EC=y,则FC=x,AF=y,FE=y-x,AE=$\sqrt{13}$x.
在Rt△AEF中,由勾股定理得:AE2=EF2+AF2,即$(\sqrt{13}x)^{2}=(y-x)^{2}+{y}^{2}$,
整理得:6x2+xy-y2=0,
∴(2x+y)(3x-y)=0.
∴$\frac{x}{y}=\frac{1}{3}$或$\frac{x}{y}=-\frac{1}{2}$(舍去).
∴tan∠BCE=$\frac{BE}{EC}=\frac{x}{y}=\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题主要考查的是全等三角形的性质和判定、勾股定理、锐角三角函数的定义以及因式分解法解方程,在Rt△AEF中,由勾股定理得建立方程是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
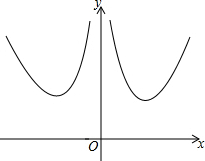 函数y=x2+$\frac{4}{{x}^{2}}$的图象如图所示,关于该函数下列结论正确的是①②③(填序号).
函数y=x2+$\frac{4}{{x}^{2}}$的图象如图所示,关于该函数下列结论正确的是①②③(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
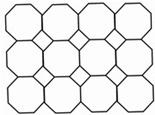 如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要12个小正方形,14小三角形.(不含图案的4个角)
如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要12个小正方形,14小三角形.(不含图案的4个角)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
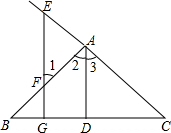 看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com