
【题目】如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在直线AB上.
(1)试说明∠1,∠2,∠3之间的关系式;(要求写出推理过程)
(2)如果点P在A、B两点之间(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系是否发生变化?(只回答)
(3)如果点P在A、B两点外侧(点P和A、B不重合)运动时,试探究∠1,∠2,∠3之间的关系.(要求写出推理过程)
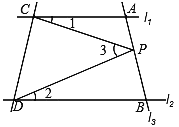
【答案】(1)∠1+∠2=∠3,理由见解析;(2)同(1)可证∠1+∠2=∠3;(3)∠1-∠2=∠3或∠2-∠1=∠3,理由见解析
【解析】试题分析:(1)过点P作l1的平行线,根据平行线的性质进行解题;(2)(3)都是同样的道理.
试题解析:(1)∠1+∠2=∠3;
理由:过点P作l1的平行线,
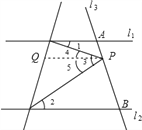
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(2)∠1+∠2=∠3;
理由:过点P作l1的平行线,

∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(3)∠1-∠2=∠3或∠2-∠1=∠3,
理由:当点P在下侧时,过点P作l1的平行线PQ,
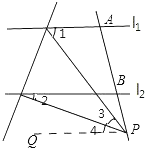
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)
∴∠1-∠2=∠3;
当点P在上侧时,同理可得:∠2-∠1=∠3.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E为AB的中点,AC与DE交于点F.
,E为AB的中点,AC与DE交于点F.

(1)求证: ![]() =AB·AD;
=AB·AD;
(2)求证:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有![]() 个白球、
个白球、![]() 个蓝球;乙盒中有
个蓝球;乙盒中有![]() 个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的
个白球、若干个蓝球,从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的![]() 倍.
倍.
(![]() )求乙盒中蓝球的个数.
)求乙盒中蓝球的个数.
(![]() )从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A. x1=1,x2=-1 B. x1=1,x2=2 C. x1=1,x2=0 D. x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
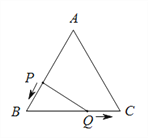
【题目】如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP![]() cm,BQ
cm,BQ![]() cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(-4,0),B(2,6)两点.
(1)求一次函数y=kx+b的表达式;
(2)在直角坐标系中,画出这个函数的图象;
(3)求这个一次函数与坐标轴围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com