
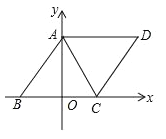
【题目】如图,平行四边形ABCD的顶点A在y轴的正半轴上,坐标原点O在边BC上,AD=6,OA、OB的长分别是关于x的一元二次方程x2﹣7x+12=0的两个根.且OA>OB.
(1)求点C、D的坐标.
(2)求证:射线AO是∠BAC的平分线.
【答案】(1)C(3,0),D(6,4);(2)证明见解析.
【解析】
(1)先利用因式分解法解方程x2﹣7x+12=0得到OA=4,OB=3,再利用平行四边形的性质得AD∥BC,BC=AD=6,则OC=3,从而得到C、D的坐标;
(2)先证明AO垂直平分BC得到AB=AC,然后根据等腰三角形的性质得到结论.
(1)∵x2﹣7x+12=0,(x﹣3)(x﹣4)=0,
∴x1=3,x2=4,
∴OA=4,OB=3.
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD=6,
∴OC=6﹣3=3,
∴D(6,4),C(3,0);
(2)∵OB=OC,AO⊥BC,即AO垂直平分BC,
∴AB=AC,
∴射线AO是∠BAC的平分线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
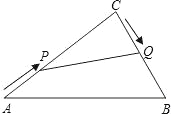
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以点C、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
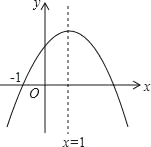
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A. ac>0
B. 当x>1时,y随x的增大而增大
C. 2a+b=1
D. 方程ax2+bx+c=0有一个根是x=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
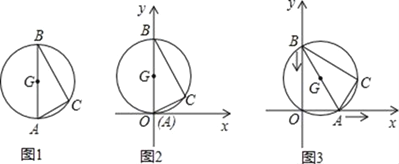
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )
A. 4 B. 6 C. 4![]() ﹣2 D. 10﹣4
﹣2 D. 10﹣4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数y=x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|x+b|(b为常数)的图象
(1)当b=0时,在同一直角坐标系中分别画出函数![]() 与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,
与y=|x+b|的图象,并利用这两个图象回答:x取什么值时,![]() 比|x|大?
比|x|大?
(2)若函数y=|x+b|(b为常数)的图象在直线y=1下方的点的横坐标x满足0<x<3,直接写出b的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
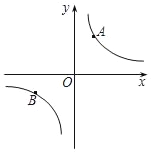
【题目】如图,A(1,y1)、B(﹣2,y2)是双曲线y=![]() 上两点,且y1+y2=1.
上两点,且y1+y2=1.
(1)求双曲线y=![]() 的解析式;
的解析式;
(2)若点C的坐标为(0,﹣1)时,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com