
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束. 在整个运动过程中,点C运动的路程是( )
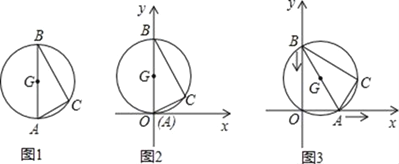
A. 4 B. 6 C. 4![]() ﹣2 D. 10﹣4
﹣2 D. 10﹣4![]()
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
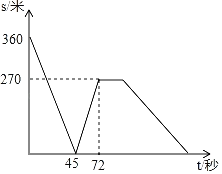
【题目】小明和小亮分别从同一直线跑道A、B两端同时相向匀速出发,小明和小亮第一次相遇后,小明觉得自己速度太慢便提速至原速的![]() 倍,并匀速运动达到B端,且小明到达B端后停止运动,小亮匀速跑步到达A端后,立即按原速返回B端(忽略调头时间),回到B端后停止运动,已知两人相距的路程S(千米)与小亮出发时间t(秒)之间的关系如图所示,则当小明到达B端后,经过_____秒,小亮回到B端.
倍,并匀速运动达到B端,且小明到达B端后停止运动,小亮匀速跑步到达A端后,立即按原速返回B端(忽略调头时间),回到B端后停止运动,已知两人相距的路程S(千米)与小亮出发时间t(秒)之间的关系如图所示,则当小明到达B端后,经过_____秒,小亮回到B端.
查看答案和解析>>
科目:初中数学 来源: 题型:
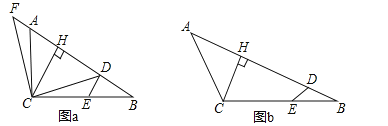
【题目】如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F.
①求证:FA=DE;
②请猜想三条线段DE,AD,CH之间的数量关系,直接写出结论;
(2)如图b,当∠ACB=120°时,三条线段DE,AD,CH之间存在怎样的数量关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
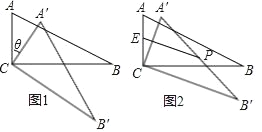
【题目】在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A'B'C.
(1)如图1,当AB∥CB'时,设A'B'与CB相交于点D,求证:△A'CD是等边三角形.
(2)若E为AC的中点,P为A'B'的中点,则EP的最大值是多少,这时旋转角θ为多少度.
查看答案和解析>>
科目:初中数学 来源: 题型:
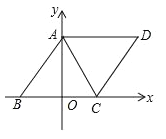
【题目】如图,平行四边形ABCD的顶点A在y轴的正半轴上,坐标原点O在边BC上,AD=6,OA、OB的长分别是关于x的一元二次方程x2﹣7x+12=0的两个根.且OA>OB.
(1)求点C、D的坐标.
(2)求证:射线AO是∠BAC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
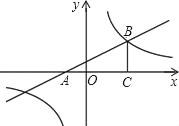
【题目】如图,平面直角坐标系中,直线y=![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 在第一象限内交于点B,BC⊥x轴于点C,OC=3AO.
在第一象限内交于点B,BC⊥x轴于点C,OC=3AO.
(1)求双曲线的解析式;
(2)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
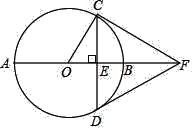
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,过点C的切线交AB的延长线于点F,连接DF.
(1)求证:DF是⊙O的切线;
(2)连接BC,若∠BCF=30°,BF=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为:A 级(非常喜欢),B 级(较喜欢),C 级(一般),D 级(不喜欢).请结合两幅统计图,回答下列问题:

(1)本次抽样调查的样本容量是 ,表示“D级(不喜欢)”的扇形的圆心角为 °;
(2)若该校九年级有200名学生.请你估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数;
(3)若从本次调查中的A级(非常喜欢)的5名学生中,选出2名去参加广州市中学生诗词大会比赛,已知A级学生中男生有3名,请用“列表”或“画树状图”的方法求出所选出的2名学生中至少有1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
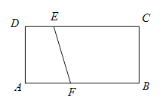
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com