
【题目】在平面直角坐标系xOy(如图)中,抛物线y=ax2+bx+2经过点A(4,0)、B(2,2),与y轴的交点为C.
(1)试求这个抛物线的表达式;
(2)如果这个抛物线的顶点为M,求△AMC的面积;
(3)如果这个抛物线的对称轴与直线BC交于点D,点E在线段AB上,且∠DOE=45°,求点E的坐标.
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)点E的坐标为(3,1).
;(3)点E的坐标为(3,1).
【解析】
(1)根据点A,B的坐标,利用待定系数法即可求出抛物线的表达式;
(2)利用配方法可求出点M的坐标,利用二次函数图象上点的坐标特征可求出点C的坐标,过点M作MH⊥y轴,垂足为点H,利用分割图形求面积法可得出△AMC的面积;
(3)连接OB,过点B作BG⊥x轴,垂足为点G,则△BGA,△OCB是等腰直角三角形,进而可得出∠BAO=∠DBO,由∠DOB+∠BOE=45°,∠BOE+∠EOA=45°可得出∠EOA=∠DOB,进而可证出△AOE∽△BOD,利用相似三角形的性质结合抛物线的对称轴为直线x=1可求出AE的长,过点E作EF⊥x轴,垂足为点F,则△AEF为等腰直角三角形,根据等腰直角三角形的性质可得出AF、EF的长,进而可得出点E的坐标.
解:(1)将A(4,0),B(2,2)代入y=ax2+bx+2,得:![]() ,
,
解得: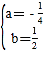 ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
(2)∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴顶点M的坐标为(1,![]() ).
).
当x=0时,y=﹣![]() x2+
x2+![]() x+2=2,
x+2=2,
∴点C的坐标为(0,2).
过点M作MH⊥y轴,垂足为点H,如图1所示.
∴S△AMC=S梯形AOHM﹣S△AOC﹣S△CHM,
=![]() (HM+AO)OH﹣
(HM+AO)OH﹣![]() AOOC﹣
AOOC﹣![]() CHMH,
CHMH,
=![]() ×(1+4)×
×(1+4)×![]() ﹣
﹣![]() ×4×2﹣
×4×2﹣![]() ×(
×(![]() ﹣2)×1,
﹣2)×1,
=![]() .
.
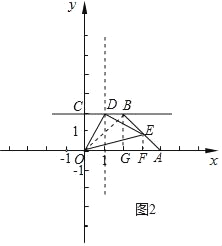
(3)连接OB,过点B作BG⊥x轴,垂足为点G,如图2所示.
∵点B的坐标为(2,2),点A的坐标为(4,0),
∴BG=2,GA=2,
∴△BGA是等腰直角三角形,
∴∠BAO=45°.
同理,可得:∠BOA=45°.
∵点C的坐标为(2,0),
∴BC=2,OC=2,
∴△OCB是等腰直角三角形,
∴∠DBO=45°,BO=2![]() ,
,
∴∠BAO=∠DBO.
∵∠DOE=45°,
∴∠DOB+∠BOE=45°.
∵∠BOE+∠EOA=45°,
∴∠EOA=∠DOB,
∴△AOE∽△BOD,
∴![]() .
.
∵抛物线y=﹣![]() x2+
x2+![]() x+2的对称轴是直线x=1,
x+2的对称轴是直线x=1,
∴点D的坐标为(1,2),
∴BD=1,
∴![]() ,
,
∴AE=![]() ,
,
过点E作EF⊥x轴,垂足为点F,则△AEF为等腰直角三角形,
∴EF=AF=1,
∴点E的坐标为(3,1).


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
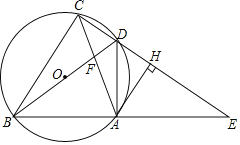
【题目】如图,在△ABC中,∠BAC=90°,点F在BC边上,过A,B,F三点的⊙O交AC于另一点D,作直径AE,连结EF并延长交AC于点G,连结BE,BD,四边形BDGE是平行四边形.
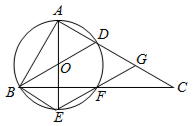
(1)求证:AB=BF.
(2)当F为BC的中点,且AC=3时,求⊙O的直径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
(1)将函数关系式用配方法化为 y=a(x+h)2+k形式,并写出它的顶点坐标、对称轴.
(2)若它的图象与x轴交于A、B两点,顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1中,△ABC为正三角形,点E为AB边上任一点,以CE为边作正△DEC,连结AD.求![]() 的值.
的值.
(2)如图2中,△ABC为等腰直角三角形,∠A=90°,点E为腰AB上任意一点,以CE为斜边作等腰直角△CDE,连结AD.求![]() 的值;
的值;
(3)如图3中,△ABC为任意等腰三角形,点E为腰AB上任意一点,以CE为底边作等腰△DEC,使△DEC∽△ABC,并且BC=![]() AC.连结AD,直接写出
AC.连结AD,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
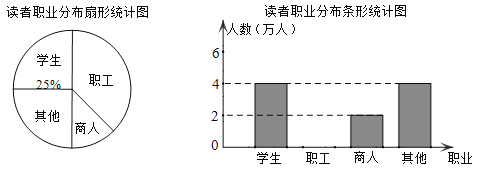
【题目】学习成为现代城市人的时尚,我市图书馆吸引了大批读者,有关部门统计了2018年第四季度到市图书馆的读者的职业分布情况,统计图如图.
(1)在统计的这段时间内,共有 万人到图书馆阅读.其中商人所占百分比是 ;
(2)将条形统计图补充完整;
(3)若今年2月到图书馆的读者共28000名,估计其中约有多少名职工.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=![]() x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;
(2)若函数y=![]() x+b(b为常数)的坐标三角形周长为16,求此三角形面积.
x+b(b为常数)的坐标三角形周长为16,求此三角形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
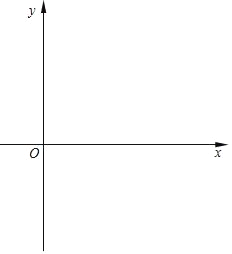
【题目】在平面直角坐标系中,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0)、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,对称轴为直线x=1,交x轴于点E,tan∠BDE=![]() .
.
(1)求抛物线的表达式;
(2)若点P是对称轴上一点,且∠DCP=∠BDE,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC、BC为直径作半圆,其中M,N分别是AC、BC为直径作半圆弧的中点,![]() ,
,![]() 的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
的中点分别是P,Q.若MP+NQ=7,AC+BC=26,则AB的长是( )
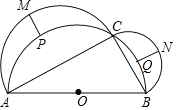
A.17B.18C.19D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com