
����Ŀ����ͼ��ʾ����ֱ������ABCD�У�AD��BC����A=90�㣬AB=12��BC=21��AD=16������P�ӵ�B������������BC�ķ�����ÿ��2����λ�����ٶ��˶�������Qͬʱ�ӵ�A���������߶�AD����ÿ��1����λ�����ٶ����D�˶���������һ�����㵽��˵�ʱ��һ������Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt���룩��
��1�����DPQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��2����tΪ��ֵʱ���ı���PCDQ��ƽ���ı��Σ�
��3���ֱ������tΪ��ֵʱ����PD=PQ����DQ=PQ��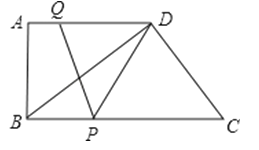
���𰸡���1���⣺ֱ������ABCD�У�AD��BC����A=90�㣬BC=21��AB=12��AD=16��
������AQ=t��BP=2t����DQ=16��t��PC=21��2t��
����P��PE��AD��E��
���ı���ABPE�Ǿ��Σ�PE=AB=12��
��S��DPQ=![]() DQAB=
DQAB=![]() ��16��t����12=��6t+96��
��16��t����12=��6t+96��
��2�����ı���PCDQ��ƽ���ı���ʱ��PC=DQ��
��21��2t=16��t��ã�t=5��
�൱t=5ʱ���ı���PCDQ��ƽ���ı��Σ�
��3����AE=BP=2t��PE=AB=12��
�ٵ�PD=PQʱ��QE=ED=![]() QD��
QD��
��DE=16��2t��
��AE=BP=AQ+QE����2t=t+16��2t��
��ã�t= ![]() ��
��
�൱t=![]() ʱ��PD=PQ
ʱ��PD=PQ
�ڵ�DQ=PQʱ��DQ2=PQ2
��t2+122=��16��t��2��ã�t=![]()
�൱t=![]() ʱ��DQ=PQ
ʱ��DQ=PQ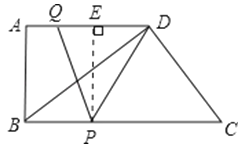
����������1��S��QDP=![]() DQAB��������֪��AQ=t��DQ=AD��AQ=16��t����DQ��AB�ij����룬�����S��t֮��ĺ�����ϵʽ��
DQAB��������֪��AQ=t��DQ=AD��AQ=16��t����DQ��AB�ij����룬�����S��t֮��ĺ�����ϵʽ��
��2�����ı���PCDQΪƽ���ı���ʱ��PC=DQ����16��t=21��2t���ɽ�t�����
��3����PD=PQʱ���ɵã�AD=3t���Ӷ��ɽ�t�������DQ=PQʱ������DQ2=PQ2����t2+122=��16��t��2�ɽ�t�����


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����λΪ1�ķ���ֽ�ϣ���A1A2A3����A3A4A5����A5A6A7��������б����x���ϡ�б�߳��ֱ�Ϊ2��4��6�����ĵ���ֱ�������Σ�����A1A2A3�Ķ�������ֱ�ΪA1(2��0)��A2(1��-1)��A3(0��0)������ͼ����ʾ���ɣ�A2017�ĺ�����Ϊ�� ��

A. 1010 B. 2 C. 1 D. ��1006
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ���ADΪ�ҵġ�O��AB��AC��E��F����֪EF��BC.
��1����֤��BC�ǡ�O�����ߣ�
��2������֪AE=9��CF=4����DE����
��3���ڣ�2���������£�����BAC=60������tan��AFE��ֵ��GD��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2017��ˮ������Ϊ100�֣�2019��ˮ������Ϊ196�֣���ù�ˮ����������ƽ�������ʣ���ù�ˮ����������ƽ��������Ϊx�������������з���Ϊ��������
A. 196��1��x��2B. 100��1��x��2=196;C. 196��1+x��2=100;D. 100��1+x��2=196
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������е����߾�����ȵĵ��ǣ�������
A. �����ߵ��д��߽��� B. �����߽���
C. �������߽��� D. ������ƽ���ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������50Ԫ�ij˳���Ʊ����������˳˳��Ĵ�����m��ʾ�����¼��ÿ�γ˳�������nԪ�������
����m | ���n��Ԫ�� |
1 | 50��0.8 |
2 | 50��1.6 |
3 | 50��2.4 |
4 | 50��3.2 |
�� | �� |
��1��д�����˳˳��Ĵ���m��ʾ���n�Ĺ�ʽ��
��2������������ʽ�����㣺����13�γ���ʣ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧУѧ����ɲ���Уѧ���ᳫ���ġ����С���Ը������г������飬�õ�һ��ѧ�������������ݣ���ͼ�Ǹ����������ݻ��Ƶ�ͳ��ͼ��ͼ�д����Ҹ������θ߶�֮��Ϊ3��4��5��8��2����֪�˴ε����о�15Ԫ��20Ԫ��������39�ˣ�
��1������һ������˶����ˣ�
��2������У����2310��ѧ���������ȫУѧ����������Ԫ��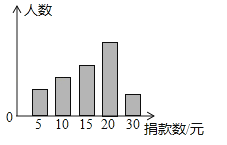
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���AC�ϵ����㣬��1=��2��
��1����֤��AE=CF��
��2����֤���ı���EBFD��ƽ���ı��Σ�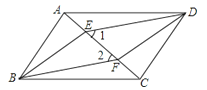
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=kx��k��0���ĺ���ֵy��x���������С����һ�κ���y=kx+k��ͼ�������ͼ�еģ�������
A.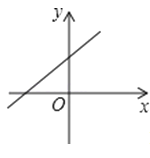
B.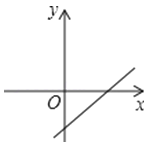
C.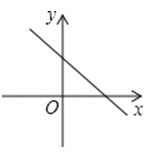
D.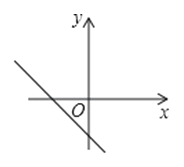
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com