Question

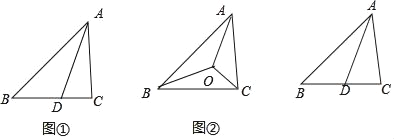
【题目】（发现）(1)如图1，在△ABC中，AD是∠BAC的平分线，对于以下结论：

①AD是△ABC的中线；②S△ABD：S△ACD＝AB：AC；③AB：AC＝BD：DC,

其中正确的是　 　(只填序号)

（探究）(2)请你选择(1)中正确的一个选项，简述理由

（应用）(3)如图2，△ABC的三个内角的角平分线相交于点O，且AB＝40，BC＝48，AC＝32，则SABO：S△BCO：S△ACO＝　 　：　 　：　 　

（拓展）(4)在(1)中的条件下，过点D作DE⊥AB于点E，DF⊥AB于点F，连接EF，求证：AD垂直平分EF．

Answer 1

【答案】(1)②③；(2)见解析；(3)5，6，4；(4)证明见解析.

【解析】

（1）根据角平分线的性质和三角形面积公式逐一判断可得；

（2）②由AD平分∠BAC知点D到AB、AC的距离相等，设为h，由S△ABD=ABh，S△ACD=ACh可判断结论②；③作AP⊥BC，由S△ABD=BDAP，S△ACD=CDAP知S△ABD：S△ACD=BD：CD，结合S△ABD：S△ACD=AB：AC可得答案；

（3）作OE⊥AB于E，OF⊥BC于F，OG⊥AC于G，根据角平分线的性质知OE=OF=OG，根据S△ABO=ABOE，S△BCO=BCOF，S△ACO=ACOG可得答案；

（4）根据角平分线上的点到角的两边的距离相等可得DE=DF，再利用“HL”证明△ADE和△ADF全等，根据全等三角形的可得AE=AF，再利用等腰三角形的证明即可．

(1)正确的是②③，

故答案为：②③．

(2)②∵AD平分∠BAC，

∴点D到AB、AC的距离相等，设为h，

则S△ABD＝ABh，S△ACD＝ACh，

∴S△ABD：S△ACD＝AB：AC；

③如图1，作AP⊥BC于点P，

则S△ABD＝BDAP，S△ACD＝CDAP，

∴S△ABD：S△ACD＝BD：CD，

又∵S△ABD：S△ACD＝AB：AC，

∴AB：AC＝BD：CD．

(3)如图2，过点O作OE⊥AB于E，OF⊥BC于F，OG⊥AC于G，

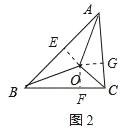
∵AO，BO，CO分别平分∠BAC，∠ABC，∠ACB，

∴OE＝OF＝OG，

∵S△ABO＝ABOE，S△BCO＝BCOF，S△ACO＝ACOG，

∴SABO：S△BCO：S△ACO＝AB：BC：AC＝40：48：32＝5：6：4，

故答案为：5：6：4；

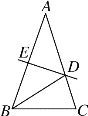
(4)如图3，

∵AD平分∠BAC，DE⊥AB，DF⊥AC，

∴DE＝DF，

在△ADE和△ADF中，

∵，

∴△ADE≌△ADF(HL)，

∴AE＝AF，

又∵AD平分∠BAC，

∴AD垂直平分EF．