
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).
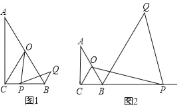
【答案】(1) BQ=CP.理由见解析;(2) 成立:PC=BQ, 理由见解析.
【解析】
(1)由∠ACB=90°,∠A=30°得到∠ABC=60°,根据直角三角形斜边上中线性质得到OB=OC,则可判断△OCB、△CPH为等边三角形,作辅助线PH∥AB交CO于H,证明△POH≌△QPB全等可得PH=QB= PC;
(2)与(1)的证明方法同样得到△POH≌△QPB,可得PH=QB= PC。
解:(1)结论:BQ=CP.
理由:如图1中,作PH∥AB交CO于H.

在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,
∴CO=AO=BO,∠CBO=60°,
∴△CBO是等边三角形,
∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,
∴∠CHP=∠CPH=60°,
∴△CPH是等边三角形,
∴PC=PH=CH,
∴OH=PB,
∵∠OPB=∠OPQ+∠QPB=∠OCB+∠COP,
∵∠OPQ=∠OCP=60°,
∴∠POH=∠QPB,
∵在△POH与△QPB中
![]() ,
,
∴△POH≌△QPB(SAS),
∴PH=QB,
∴PC=BQ.
(2)成立:PC=BQ.
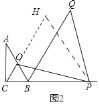
理由:作PH∥AB交CO的延长线于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,
∴CO=AO=BO,∠CBO=60°,
∴△CBO是等边三角形,
∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,
∴∠CHP=∠CPH=60°,
∴△CPH是等边三角形,
∴PC=PH=CH,
∴OH=PB,
∵∠POH=60°+∠CPO,∠QPO=60°+∠CPQ,
∴∠POH=∠QPB,
∵在△POH与△QPB中
![]() ,
,
∴△POH≌△QPB(SAS),
∴PH=QB,
∴PC=BQ.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
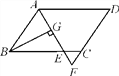
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BPPC的值为多少?若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPiPiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC,CA=CB=6cm,AB=8cm,点O为△ABC内一点(点O不在△ABC边界上).请你运用图形旋转和“两点之间线段最短”等数学知识、方法,求出OA+OB+OC的最小值为_____.
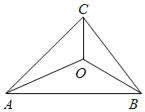
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.(1)计算AB的长等于__,(2)请在如图所示的网格中,用无刻度的直尺,画出一个△ADE,使△ADE~△ABC,且满足点D在AC边上,点E在AB边上,AE=2.简要说明画图方法(不要求证明)__.
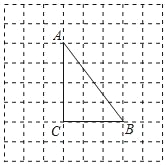
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定:转动两个转盘停止后,指针必须指到某一数字,否则重转.
(1)请用树状图或列表法列出所有可能的结果;
(2)若指针所指的两个数字都是方程x2-5x+6=0的解时,则甲获胜;若指针所指的两个数字都不是方程x2-5x+6=0的解时,则乙获胜,问他们两人谁获胜的概率大?请分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(1)求b、c的值;
(2)若只沿y轴上下平移该抛物线后与y轴的交点为A1,顶点为M1,且四边形AMM1A1是菱形,写出平移后抛物线的表达式.
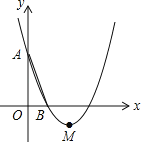
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com