
【题目】综合题
阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程![]() ,则
,则![]() ,∴
,∴![]()
求![]() 、
、![]() .则有
.则有![]() ,∴
,∴![]() .解得
.解得![]() ,
,![]() .
.![]() 则有
则有![]() ,∴
,∴![]() .解得
.解得![]() 或
或![]() ,根据以上材料解答下列各题:
,根据以上材料解答下列各题:
![]() 若
若![]() .求
.求![]() 的值.
的值.
![]() .求
.求![]() 的值.
的值.
![]() 若
若![]() .求
.求![]() 的值.
的值.
![]() 若
若![]() ,
,![]() ,
,![]() 表示
表示![]() 的三边,且
的三边,且![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
科目:初中数学 来源: 题型:
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系满足:m=﹣2t+96.且未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=![]() t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣![]() t+40(21≤t<40且t为整数).下面我们就来研究销售这种商品的有关问题
t+40(21≤t<40且t为整数).下面我们就来研究销售这种商品的有关问题
(1)请分别写出未来40天内,前20天和后20天的日销售利润w(元)与时间t的函数关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列说法,其中正确的是( )
①关于![]() 的一元二次方程
的一元二次方程![]() ,若
,若![]() ,则方程
,则方程![]() 一定没有实数根;
一定没有实数根;
②关于![]() 的一元二次方程
的一元二次方程![]() ,若
,若![]() ,则方程
,则方程![]() 必有实数根;
必有实数根;
③若![]() 是方程
是方程![]() 的根,则
的根,则![]() ;
;
④若![]() ,
,![]() ,
,![]() 为三角形三边,方程
为三角形三边,方程![]() 有两个相等实数根,则该三角形为直角三角形.
有两个相等实数根,则该三角形为直角三角形.
A. ①② B. ①④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为![]() 米的篱笆围成.已知墙长为
米的篱笆围成.已知墙长为![]() 米(如图),设这个苗圃园垂直于墙的一边长为
米(如图),设这个苗圃园垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() ;
;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值吗?如果有,求出最大值;如果没有,请说明理由.
米,这个苗圃园的面积有最大值吗?如果有,求出最大值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
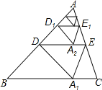
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,还原纸片后,再将
,还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ;若
;若![]() ,则
,则![]() 的值为________.
的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com