
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系满足:m=﹣2t+96.且未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=![]() t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣
t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=﹣![]() t+40(21≤t<40且t为整数).下面我们就来研究销售这种商品的有关问题
t+40(21≤t<40且t为整数).下面我们就来研究销售这种商品的有关问题
(1)请分别写出未来40天内,前20天和后20天的日销售利润w(元)与时间t的函数关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
【答案】(1)w=![]() ;(2)第19天日销售利润最大,最大利润为841元;(3)0.5≤a<4.
;(2)第19天日销售利润最大,最大利润为841元;(3)0.5≤a<4.
【解析】
(1)根据利润(w)=日销售量(m)![]() 价格差(
价格差(![]() -20)分别计算即可得出前20天和后20天的日销售利润w(元)与时间t的函数关系式;(2)根据二次函数的性质,求出(1)中的两个二次函数的最大值进行比较即可;(3)根据题意得出扣除捐赠后的利(w)与时间(t)的解析式,找出对称轴进行分析即可,
-20)分别计算即可得出前20天和后20天的日销售利润w(元)与时间t的函数关系式;(2)根据二次函数的性质,求出(1)中的两个二次函数的最大值进行比较即可;(3)根据题意得出扣除捐赠后的利(w)与时间(t)的解析式,找出对称轴进行分析即可,
(1)当1≤t≤20且t为整数时,
w=(![]() t+25﹣20)(﹣2t+96)
t+25﹣20)(﹣2t+96)
=﹣t2+38t+480;
当21≤t<40且t为整数时,
w=(﹣![]() t+40﹣20)(﹣2t+96)
t+40﹣20)(﹣2t+96)
=t2﹣88t+1920,
综上w=![]() .
.
(2)当1≤t≤20且t为整数时,w=﹣t2+38t+480=﹣(t﹣19)2+841,
此时当t=19时,w取得最大值841;
当21≤t<40且t为整数时,w=t2﹣88t+1920=(t﹣44)2﹣16,
∵t<44时,w随t的增大而减小,
∴当t=21时,w取得最大值,最大值为513;
综上,第19天日销售利润最大,最大利润为841元.
(3)根据题意知,扣除捐款后的利润w=﹣t2+38t+480﹣(﹣2t+96)a
=﹣t2+(38+2a)t+480﹣96a
∴﹣1<0,且对称轴t=19+a,
因为t为整数,所以函数图象是为20个分布在抛物线上的散点,要使日销售利润随时间t增大而增大,
则要求对称轴19+a≥19.5,
解得a≥0.5,
又a<4,
则0.5≤a<4.


科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,点D是斜边AB的中点,点E从点B出发以1cm/s的速度向点C运动,点F同时从点C出发以一定的速度沿射线CA方向运动,规定:当点E到终点C时停止运动;设运动的时间为x秒,连接DE、DF.
(1)填空:S△ABC= cm2;
(2)当x=1且点F运动的速度也是1cm/s时,求证:DE=DF;
(3)若动点F以3cm/s的速度沿射线CA方向运动;在点E、点F运动过程中,如果有某个时间x,使得△ADF的面积与△BDE的面积存在两倍关系,请你直接写出时间x的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )

A.(﹣2,﹣3)B.(2,﹣3)C.(2,3)D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自![]() 年
年![]() 月
月![]() 日零时起,高铁开通,某旅行社为吸引广大市民组团去仙都旅游,推出了如下收费标准:如果人数不超过
日零时起,高铁开通,某旅行社为吸引广大市民组团去仙都旅游,推出了如下收费标准:如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元,如果人数超过
元,如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
![]() 如果某单位组织
如果某单位组织![]() 人参加仙都旅游,那么需支付旅行社旅游费用________元;
人参加仙都旅游,那么需支付旅行社旅游费用________元;
![]() 现某单位组织员工去仙都旅游,共支付给该旅行社旅游费用
现某单位组织员工去仙都旅游,共支付给该旅行社旅游费用![]() 元,那么该单位有多少名员工参加旅游?
元,那么该单位有多少名员工参加旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程![]() ,则
,则![]() ,∴
,∴![]()
求![]() 、
、![]() .则有
.则有![]() ,∴
,∴![]() .解得
.解得![]() ,
,![]() .
.![]() 则有
则有![]() ,∴
,∴![]() .解得
.解得![]() 或
或![]() ,根据以上材料解答下列各题:
,根据以上材料解答下列各题:
![]() 若
若![]() .求
.求![]() 的值.
的值.
![]() .求
.求![]() 的值.
的值.
![]() 若
若![]() .求
.求![]() 的值.
的值.
![]() 若
若![]() ,
,![]() ,
,![]() 表示
表示![]() 的三边,且
的三边,且![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 度,并使各边长变为原来的
度,并使各边长变为原来的![]() 倍,得
倍,得![]() ,即如图①,我们将这种变换记为
,即如图①,我们将这种变换记为![]() .
.
![]() 如图①,对
如图①,对![]() 作变换
作变换![]() 得
得![]() ,则
,则![]() ________;直线
________;直线![]() 与直线
与直线![]() 所夹的锐角为________度;
所夹的锐角为________度;
![]() 如图②,
如图②,![]() 中,
中,![]() ,
,![]() ,对
,对![]() 作变换
作变换![]() 得
得![]() ,使点
,使点![]() 、
、![]() 、
、![]() 在同一直线上,且四边形
在同一直线上,且四边形![]() 为矩形,求
为矩形,求![]() 和
和![]() 的值;
的值;
![]() 如图③,
如图③,![]() ,
,![]() ,
,![]() ,对
,对![]() 作变换
作变换![]() 得
得![]() ,使点
,使点![]() 、
、![]() 、
、![]() 在同一直线上,且四边形
在同一直线上,且四边形![]() 为平行四边形,求
为平行四边形,求![]() 和
和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:
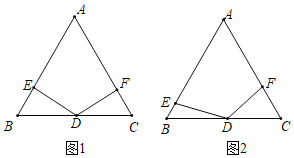
问题初探:(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为 ;
问题再探:(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:
①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.
成果运用:(3)若边长AB=8,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L 取最大值和最小值时E点的位置?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com