
����Ŀ���ڵȱ�������ABC�У���D��BC���е㣬��E��F�ֱ��DZ�AB��AC�����߶�AB��AC�Ķ˵㣩�ϵĶ��㣬�ҡ�EDF��120����С����С�۶����ͼ��չ�������о���
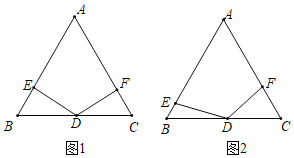
�����̽����1����ͼ1��С�����֣�����DEB��90��ʱ��BE+CF��nAB����n��ֵΪ�� ����
������̽����2����ͼ2���ڵ�E��F���˶������У�С�۷���������Ȥ�Ľ��ۣ�
��DEʼ�յ���DF����BE��CF�ĺ�ʼ�ղ��䣻����ѡ������һ�����ۼ���֤����
�ɹ�����:��3�����߳�AB��8���ڵ�E��F���˶������У����ı���DEAF���ܳ�ΪL��L��DE+EA+AF+FD�����ܳ�L ȡ���ֵ����СֵʱE���λ��?
���𰸡���1��![]() ����2���ټ��������ڼ���������3���ܳ�L ȡ���ֵʱ��E�͵�B�غϻ�BE=4��ȡ��СֵʱBE=2��
����2���ټ��������ڼ���������3���ܳ�L ȡ���ֵʱ��E�͵�B�غϻ�BE=4��ȡ��СֵʱBE=2��
��������
��1�������õȱ��������жϳ�BD=CD=![]() AB�������жϳ�BE=
AB�������жϳ�BE=![]() BD�����жϳ���DFC=90�����ó�CF=
BD�����жϳ���DFC=90�����ó�CF=![]() CD�����ɵó����ۣ�
CD�����ɵó����ۣ�
��2���ٹ������EDG�ա�FDH��ASA�����ó�DE=DF�����ɵó����ۣ�
���ɣ�1��֪��BG+CH=![]() AB���ɢ�֪����EDG�ա�FDH��ASA�����ó�EG=FH�����ɵó����ۣ�
AB���ɢ�֪����EDG�ա�FDH��ASA�����ó�EG=FH�����ɵó����ۣ�
��3���ɣ�1����2���жϳ�L=2DE+12�����жϳ�DE��ABʱ��L��С����F�͵�C�غ�ʱ��DE����ɵó����ۣ�
�⣺��1���ߡ�ABC�ǵȱ������Σ�
���B=��C=60����AB=BC��
�ߵ�D��BC���е㣬
��BD=CD=![]() BC=
BC=![]() AB��
AB��
�ߡ�DEB=90����
���BDE=90��-��B=30����
��Rt��BDE��BE=![]() BD��
BD��
�ߡ�EDF=120������BDE=30����
���CDF=180��-��BDE-��EDF=30����
�ߡ�C=60����
���DFC=90����
��Rt��CFD��CF=![]() CD��
CD��
��BE+CF=![]() BD+
BD+![]() CD=
CD=![]() BC=
BC=![]() AB��
AB��
��BE+CF=nAB��
��n=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ��
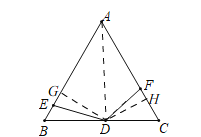
�ٹ���D��DG��AB��G��DH��AC��H��
���DGB=��AGD=��CHD=��AHD=90����
�ߡ�ABC�ǵȱ������Σ�
���A=60����
���GDH=360��-��AGD-��AHD-��A=120����
�ߡ�EDF=120����
���EDG=��FDH��
�ߡ�ABC�ǵȱ������Σ���D��BC���е㣬
���BAD=��CAD��
��DG��AB��DH��AC��
��DG=DH��
�ڡ�EDG�͡�FDH�У�
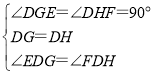 ��
��
���EDG�ա�FDH��ASA����
��DE=DF��
����DEʼ�յ���DF��
��ͬ��1���ķ����ã�BG+CH=![]() AB��
AB��
�ɢ�֪����EDG�ա�FDH��ASA����
��EG=FH��
��BE+CF=BG-EG+CH+FH=BG+CH=![]() AB��
AB��
��BE��CF�ĺ�ʼ�ղ��䣻
��3���ɣ�2��֪��DE=DF��BE+CF=![]() AB��
AB��
��AB=8��
��BE+CF=4��
���ı���DEAF���ܳ�ΪL=DE+EA+AF+FD
=DE+AB-BE+AC-CF+DF
=DE+AB-BE+AB-CF+DE
=2DE+2AB-��BE+CF��
=2DE+2��8-4
=2DE+12��
��DE���ʱ��L���DE��Сʱ��L��С��
��DE��ABʱ��DE��С��L��С��
��ʱ��BDE=90��-60��=30����
BE=![]() BD=2��
BD=2��
����F�͵�C�غϻ��E�͵�B�غ�ʱ��DE���F�͵�C�غ�ʱ����BDE=180��-��EDF=120��=60����
�ߡ�B=60����
���B=��BDE=��BED=60����
���BDE�ǵȱ������Σ�
��BE=DE=BD=![]() AB=4��
AB=4��
����E�͵�B�غ�ʱ��DE=BD=4���ܳ�L �����ֵ��
���ܳ�L ȡ���ֵʱ��E�͵�B�غϻ�BE=4��ȡ��СֵʱBE=2��


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ij��ʱ����Ʒÿ���ɱ�Ϊ20Ԫ�������г����з��֣�������Ʒ��δ��40���ڵ���������m��������ʱ��t���죩�Ĺ�ϵ���㣺m=��2t+96����δ��40���ڣ�ǰ20��ÿ��ļ۸�y1��Ԫ/������ʱ��t���죩�ĺ�����ϵʽΪy1=![]() t+25��1��t��20��tΪ����������20��ÿ��ļ۸�y2��Ԫ/������ʱ��t���죩�ĺ�����ϵʽΪy2=��
t+25��1��t��20��tΪ����������20��ÿ��ļ۸�y2��Ԫ/������ʱ��t���죩�ĺ�����ϵʽΪy2=��![]() t+40��21��t��40��tΪ���������������Ǿ����о�����������Ʒ���й�����
t+40��21��t��40��tΪ���������������Ǿ����о�����������Ʒ���й�����
��1����ֱ�д��δ��40���ڣ�ǰ20��ͺ�20�������������w��Ԫ����ʱ��t�ĺ�����ϵʽ��
��2����Ԥ��δ��40������һ������������������������������Ƕ��٣�
��3����ʵ�����۵�ǰ20���У��ù�˾����ÿ����һ����Ʒ�;���aԪ����a��4����ϣ�����̣���˾ͨ�����ۼ�¼���֣�ǰ20���У�ÿ��۳��������������������ʱ��t���죩�������������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ�DΪBC����һ�����㣨D��B��C�����غϣ���AD=AE����DAE=60��������CE��
��1����֤����ABD�ա�ACE��
��2����֤��CEƽ�֡�ACF��
��3����AB=2�����ı���ADCE���ܳ�ȡ��Сֵʱ����BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() ���ĸ��������㣺ÿһ�����㵽���������������֮������ȣ����ı���
���ĸ��������㣺ÿһ�����㵽���������������֮������ȣ����ı���![]() һ���ǣ� ��
һ���ǣ� ��
A. ������ B. ���� C. �������� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC��

(1)��������ֱ�ߺ�Բ��������²�����
������ABC�Ľ�ƽ����AD��
������AB�Ĵ�ֱƽ����EF��EF��AD�ཻ�ڵ�P��
������PB��PC��
����۲�ͼ�ν���������⣺
��2���߶�PA��PB��PC֮���������ϵ���� ������˵�����ɣ�
��3������ABC��70�������BPC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶ij��Ϊ���Ƽ��ڱ��õĽ�Ʒ���ƻ������곬�й���ʼDZ���ˮ�ʹ�40�����ڻ�֪ij����������һ������������Ӹ����깺����Щ��Ʒ����֪�ʼDZ���ˮ�����������̵�����ۼ۷ֱ����±����������곬�й�����Щ��Ʒ�軨��90Ԫ��
Ʒ���̵� | �ʼDZ���Ԫ/���� | ˮ�ʣ�Ԫ/���� |
���곬�� | 2.4 | 2 |
���� | 2 | 1.8 |
��1��������蹺��ʼDZ���ˮ�ʵ�������
��2��������깺����Щ��Ʒ�ɽ�ʡ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ���Ź�
���Ź�![]() �е�
�е�![]() ��ֱ���۵���ʹ��
��ֱ���۵���ʹ��![]() ����
����![]() ���ϵ�
���ϵ�![]() ������Ϊ��
������Ϊ��![]() �β������ۺ�
�β������ۺ�![]() ��
��![]() �ľ����Ϊ
�ľ����Ϊ![]() ����ԭֽƬ���ٽ�
����ԭֽƬ���ٽ�![]() ���Ź�
���Ź�![]() �е�
�е�![]() ��ֱ���۵���ʹ��
��ֱ���۵���ʹ��![]() ����
����![]() ���ϵ�
���ϵ�![]() ������Ϊ��
������Ϊ��![]() �β������ۺ�
�β������ۺ�![]() ��
��![]() �ľ����Ϊ
�ľ����Ϊ![]() ���������������ϲ�����ȥ����������
���������������ϲ�����ȥ����������![]() �β�����õ����ۺ�
�β�����õ����ۺ�![]() ����
����![]() �ľ����Ϊ
�ľ����Ϊ![]() ����
����![]() ����
����![]() ��ֵΪ________��
��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD�Ǹߣ�AE��BF�ǽ�ƽ���ߣ������ཻ�ڵ�O����BAC=50�㣬��C=70�������DAC�͡�BOA�Ķ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����1��5����B����1��0����C����4��3����

��1���뻭����ABC����y��ԳƵġ�DEF������D��E��F�ֱ���A��B��C�Ķ�Ӧ�㣩��
��2��ֱ��д����1����F�������Ϊ�� ����
��3����ֱ��l�����㣨0����2������x��ƽ�У����C����ֱ��l�ĶԳƵ������Ϊ�� ����
��4����y���ϴ���һ��P��ʹPC��PB������P������Ϊ�� ����
��5����һ������һ��M��4��2������x������һ��QʹCQ+MQ��̣��������·����������ͼ�ۼ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com