
【题目】如图,△ABC中,AB=AC,

(1)请你利用直尺和圆规完成如下操作:
①作△ABC的角平分线AD;
②作边AB的垂直平分线EF,EF与AD相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(2)线段PA,PB,PC之间的数量关系是 ;请说明理由.
(3)若∠ABC=70°,求∠BPC的度数.
【答案】(1)见解析;(2)PA=PB=PC,理由见解析;(3)80°.
【解析】
(1)利用基本作图作角平分线AD和AB的垂直平分线,它们相交于P点;
(2)根据线段的垂直平分线的性质可得:PA=PB=PC;
(3)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=180°-2×70°=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.
解:(1)如图,AD、EF 、点P为所作;
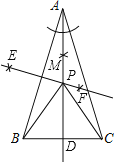
(2)PA=PB=PC,理由:
∵AB=AC,AD平分∠BAC,
∴AD是BC的垂直平分线,
∴PB=PC,
∵EP是AB的垂直平分线,
∴PA=PB,
∴PA=PB=PC;
故答案为:PA=PB=PC;
(3)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠BAC=180°-2×70°=40°,
∵AM平分∠BAC,
∴∠BAD=∠CAD=20°,
∵PA=PB=PC,
∴∠ABP=∠BAP=∠ACP=20°,
∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若AB=6,sin∠BAC=![]() ,求BE的长.
,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.

(1)请你写出图中所有的等腰三角形;
(2)请你判断AD与BE垂直吗?并说明理由.
(3)如果BC=10,求AB+AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
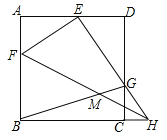
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形.

(1)图b中的阴影部分面积为 ;
观察图b,请你写出三个代数式![]() ,
,![]() ,mn之间的等量关系是 ;
,mn之间的等量关系是 ;
(3)若x+y=﹣6,xy=2.75,利用提供的等量关系计算:x﹣y= ;
(4)实际上有许多代数恒等式可以用图形的面积来表示,如图C,它表示了2![]() +3mn+
+3mn+![]() =(m+n)(2m+n),试画出一个几何图形的面积是
=(m+n)(2m+n),试画出一个几何图形的面积是![]() +4ab+3
+4ab+3![]() ,并能利用这个图形将
,并能利用这个图形将![]() +4ab+3
+4ab+3![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有关部门从甲、乙两个城市所有的自动售货机中分别随机抽取了16台,记录下某一天各自的销售情况(单位:元):
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23
小强用如图所示的方法表示甲城市16台自动售货机的销售情况.
(1)请你仿照小强的方法将乙城市16台自动售货机的销售情况表示出来;
(2)请你观察图1,你能从图1中获取哪些信息?(至少写出两条不同类型信息)
(3)小芳用图2的条形统计图表示甲城市16台自动售货机的销售情况,请你观察图2,你能从图2中获取哪些信息?(至少写出两条不同类型信息)
(4)如果收集到的数据很多,例如有200个,你认为图1和图2这两种统计图用哪一种更能直观的反映这些数据分布的大致情况?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com