
【题目】如图,在![]() 中,
中,![]() 分别垂直平分
分别垂直平分![]() 和
和![]() ,交
,交![]() 于
于![]() 两点,
两点,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)若![]() =21cm,则
=21cm,则![]() 的周长= ;(第一问直接写答案)
的周长= ;(第一问直接写答案)
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)21cm;(2)20°
【解析】
(1)根据线段的垂直平分线的性质,可知,AM=CM,BN=CN,然后,即可求出![]() 的周长;
的周长;
(2)根据三角形的内角和定理,求出∠MNF+∠NMF,进而求出∠A+∠B,根据等腰三角形的性质,可知,∠A=∠ACM,∠B=∠BCN,最后,利用三角形内角和定理,即可求解.
(1)∵![]() 分别垂直平分
分别垂直平分![]() 和
和![]() ,
,
∴AM=CM,BN=CN,
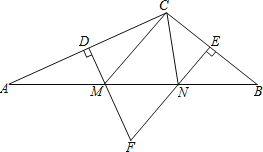
∴![]() 的周长=CM+CN+MN=AM+BN+MN=AB=21cm;
的周长=CM+CN+MN=AM+BN+MN=AB=21cm;
(2)∵![]() ,
,
∴∠MNF+∠NMF=180°-∠MFN=180°-80°=100°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=100°,
∴∠A+∠B=90°-∠AMD+90°-∠BNE=180°-100°=80°,
由(1)可知,AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=180°-2×80°=20°.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+2分别与x轴、y轴相交于点A、点B
x+2分别与x轴、y轴相交于点A、点B

(1)求点A和点B的坐标;
(2)若点P是y轴上的一点,设△AOB、△ABP的面积分别为S△AOB与S△ABP,且S△ABP=2S△AOB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
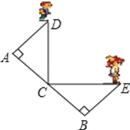
【题目】如图,C 是路段 AB 的中点,两人从 C 同时出发,以相同的速度分别沿两条直线行走,并同时到达 D,E 两地,DA⊥AB,EB⊥AB,D,E 与路段AB 的距离相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2,k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2,满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程![]() ,则
,则![]() ,∴
,∴![]()
求![]() 、
、![]() .则有
.则有![]() ,∴
,∴![]() .解得
.解得![]() ,
,![]() .
.![]() 则有
则有![]() ,∴
,∴![]() .解得
.解得![]() 或
或![]() ,根据以上材料解答下列各题:
,根据以上材料解答下列各题:
![]() 若
若![]() .求
.求![]() 的值.
的值.
![]() .求
.求![]() 的值.
的值.
![]() 若
若![]() .求
.求![]() 的值.
的值.
![]() 若
若![]() ,
,![]() ,
,![]() 表示
表示![]() 的三边,且
的三边,且![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com