
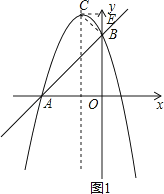
【题目】如图,已知抛物线y=﹣x2+bx+c与直线AB相交于A(﹣3,0),B(0,3)两点.
(1)求这条抛物线的解析式;
(2)设C是抛物线对称轴上的一动点,求使∠CBA=90°的点C的坐标;
(3)探究在抛物线上是否存在点P,使得△APB的面积等于3?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
【解答】解:把点A(﹣3,0),B(0,3)代入y=﹣x2+bx+c得:
![]() ,
,
解得:![]()
∴抛物线的解析式是y=﹣x2﹣2x+3;
(2)
如图1:过点B作CB⊥AB,交抛物线的对称轴于点C,过点C作CE⊥y轴,垂足为点E,
∵y=﹣x2﹣2x+3,
∴抛物线对称轴为直线x=﹣1,
∴CE=1,
∵AO=BO=3,
∴∠ABO=45°,
∴∠CBE=45°,
∴BE=CE=1,
∴OE=OB+BE=4,
∴点C的坐标为(﹣1,4);
(3)
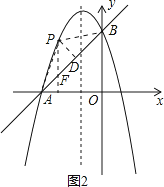
假设在在抛物线上存在点P,使得△APB的面积等于3,如图2:
连接PA,PB,过P作PD⊥AB于点D,作PF∥y轴交AB于点F,在Rt△OAB中,易求AB=![]() =
=![]() ,
,
∵S△APB=3,
∴PD=![]()
∵∠PFD=∠ABO=45°,
∴PF=2,
设点P的坐标为(m,﹣m2﹣2m+3),
∵A(﹣3,0),B(0,3),
∴直线AB的解析式为y=x+3,
∴可设点F的坐标为(m,m+3),
①当点P在直线AB上方时,
可得:﹣m2﹣2m+3=m+3+2,
解得:m=﹣1或﹣2,
∴符合条件的点P坐标为(﹣1,4)或(﹣2,3),
②当点P在直线AB下方时,
可得:﹣m2﹣2m+3=m+3﹣2,
解得:m=![]() 或
或![]() ,
,
∴符合条件的点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
综上可知符合条件的点P有4个,坐标分别为:(﹣1,4)或(﹣2,3)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】(1)把点A(﹣3,0),B(0,3)两点的坐标分别代入抛物线解析式求出b和c的值即可;
(2)过点B作CB⊥AB,交抛物线的对称轴于点C,过点C作CE⊥y轴,垂足为点E,易求点C的横坐标,再求出OE的长,即可得到点C的纵坐标;
(3)假设在在抛物线上存在点P,使得△APB的面积等于3,连接PA,PB,过P作PD⊥AB于点D,作PF∥y轴交AB于点F,在Rt△OAB中,易求AB=![]() =3
=3![]() ,设点P的坐标为(m,﹣m2﹣2m+3),设点F的坐标为(m,m+3),再分两种情况①当点P在直线AB上方时,②当点P在直线AB下方时分别讨论求出符合条件点P的坐标即可.
,设点P的坐标为(m,﹣m2﹣2m+3),设点F的坐标为(m,m+3),再分两种情况①当点P在直线AB上方时,②当点P在直线AB下方时分别讨论求出符合条件点P的坐标即可.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=k2x+b的图象交于点P(m,﹣1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.
的图象与一次函数y=k2x+b的图象交于点P(m,﹣1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ. 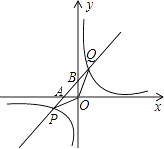
(1)求两函数的解析式;
(2)求证:△POB≌△QOA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.
请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() ,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联华商场以150元/台的价格购进某款电风扇若干台,很快售完.商场用相同的货款再次购进这款电风扇,因价格提高30元,进货量减少了10台.
(1)这两次各购进电风扇多少台?
(2)商场以250元/台的售价卖完这两批电风扇,商场获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A1 , A2 , …,An均在直线y=x﹣1上,点B1 , B2 , …,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2015= .
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=﹣1,则a2015= . 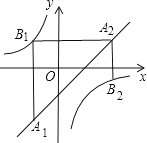
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com