
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
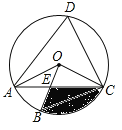
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=![]() ,求图中阴影部分面积(结果保留π和根号).
,求图中阴影部分面积(结果保留π和根号).
【答案】(1)30°;(2)![]() .
.
【解析】
试题(1)圆内接四边形性质得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,由OA=OC得到∠OAC=∠OCA=30°;
(2)由∠COB=3∠AOB得到∠AOB=30°,从而有∠COB为直角,然后利用S阴影=S扇形OBC﹣S△OEC求解.
试题解析:(1)∵四边形ABCD是⊙O的内接四边形,∴∠ABC+∠D=180°,∵∠ABC=2∠D,∴∠D+2∠D=180°,∴∠D=60°,∴∠AOC=2∠D=120°,∵OA=OC,∴∠OAC=∠OCA=30°;
(2)∵∠COB=3∠AOB,∴∠AOC=∠AOB+3∠AOB=120°,∴∠AOB=30°,∴∠COB=∠AOC﹣∠AOB=90°,在Rt△OCE中,OC=![]() ,∴OE=OCtan∠OCE=
,∴OE=OCtan∠OCE=![]() tan30°=
tan30°=![]() =2,
=2,
∴S△OEC=![]() OEOC=
OEOC=![]() =
=![]() ,∴S扇形OBC=
,∴S扇形OBC=![]() =3π,∴S阴影=S扇形OBC﹣S△OEC=
=3π,∴S阴影=S扇形OBC﹣S△OEC=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为![]() (分),与乙地的距离为
(分),与乙地的距离为![]() (米),图中线段EF,折线
(米),图中线段EF,折线![]() 分别表示两人与乙地距离
分别表示两人与乙地距离![]() 和运动时间
和运动时间![]() 之间的函数关系图象
之间的函数关系图象
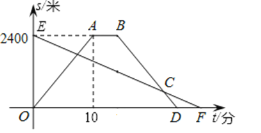
(1)李越骑车的速度为 米/分钟;F点的坐标为 ;
(2)求李越从乙地骑往甲地时, ![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)求王明从甲地到乙地时, ![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(4)求李越与王明第二次相遇时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).

(1)直接写出这两个二次函数的表达式;
(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;
(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
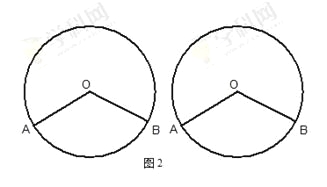
【题目】(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 .

(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=2x+2与y轴、x轴分别交于A、B两点,以B为直角顶点在第二象限作等腰Rt△ABC .
(1)求点C的坐标,并求出直线AC的关系式.
(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.
(3)如图3,在(1)的条件下,直线AC交x轴于M,P(![]() ,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的
,k)是线段BC上一点,在线段BM上是否存在一点N,使△BPN的面积等于△BCM面积的![]() ?若存在,请求出点N的坐标;若不存在,请说明理由.
?若存在,请求出点N的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
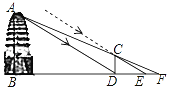
【题目】如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲,乙两组数据的折线图如图所示,设甲,乙两组数据的方差分别为S2甲,S2乙,则S2甲与S2乙大小关系为( )
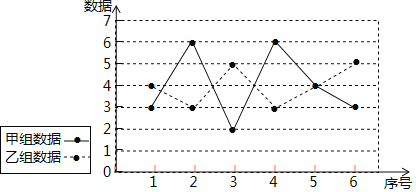
A.S2甲>S2乙B.S2甲=S2乙C.S2甲<S2乙D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com