
����Ŀ����ͼ1����ֱ֪��y=2x+2��y�ᡢx��ֱ���A��B���㣬��BΪֱ�Ƕ����ڵڶ�����������Rt��ABC ��
��1�����C�����꣬�����ֱ��AC�Ĺ�ϵʽ��
��2����ͼ2��ֱ��CB��y����E����ֱ��CB��ȡһ��D������AD����AD=AC����֤��BE=DE��
��3����ͼ3���ڣ�1���������£�ֱ��AC��x����M��P��![]() ��k�����߶�BC��һ�㣬���߶�BM���Ƿ����һ��N��ʹ��BPN�����������BCM�����
��k�����߶�BC��һ�㣬���߶�BM���Ƿ����һ��N��ʹ��BPN�����������BCM�����![]() �������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�


���𰸡���1��C����3��1����ֱ��AC��y=![]() x+2����2��֤������������3��N����
x+2����2��֤������������3��N����![]() ��0����
��0����
�������������������1����CQ��x�ᣬ����ΪQ����������֤����ABO�ա�BCQ���Ӷ����CQ=OB=1���ɵ�C����3��1�����ô���ϵ��������ֱ��AC�Ľ���ʽy=![]() x+2����2����CH��x����H��DF��x����F��DG��y����G��֤����BCH�ա�BDF����BOE�ա�DGE���ɵ�BE=DE����3�������ֱ��BC�Ľ���ʽ���Ӷ�ȷ����P�����꣬������ڵ�Nʹֱ��PNƽ����BCM�������Ȼ������BN�ij����Ƚ�BM,BN�Ĵ�С���жϵ�N�Ƿ����߶�BM�ϼ��ɣ�
x+2����2����CH��x����H��DF��x����F��DG��y����G��֤����BCH�ա�BDF����BOE�ա�DGE���ɵ�BE=DE����3�������ֱ��BC�Ľ���ʽ���Ӷ�ȷ����P�����꣬������ڵ�Nʹֱ��PNƽ����BCM�������Ȼ������BN�ij����Ƚ�BM,BN�Ĵ�С���жϵ�N�Ƿ����߶�BM�ϼ��ɣ�
����������⣺��1����ͼ1����CQ��x�ᣬ����ΪQ��
���OBA+��OAB=90������OBA+��QBC=90����
���OAB=��QBC��
����AB=BC����AOB=��Q=90����
���ABO�ա�BCQ��
��BQ=AO=2��OQ=BQ+BO=3��CQ=OB=1��
��C����3��1����
��A��0��2����C����3��1��
��֪��ֱ��AC��y=![]() x+2��
x+2��
��2����ͼ2����CH��x����H��DF��x����F��DG��y����G��
��AC=AD��AB��CB��
��BC=BD��
���BCH�ա�BDF��
��BF=BH=2��
��OF=OB=1��
��DG=OB��
���BOE�ա�DGE��
��BE=DE��
��3����ͼ3��ֱ��BC��y=��![]() x��
x��![]() ��P��
��P��![]() ��k�����߶�BC��һ�㣬
��k�����߶�BC��һ�㣬
��P����![]() ��
��![]() ������y=
������y=![]() x+2֪M����6��0����
x+2֪M����6��0����
��BM=5����S��BCM=![]() ��
��
������ڵ�Nʹֱ��PNƽ����BCM�������
��![]() BN��
BN��![]() =
=![]() ��
��![]() ��
��
��BN=![]() ��ON=
��ON=![]() ��
��
��BN��BM��
����N���߶�BM�ϣ�
��N����![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ƻ�����һƬ�յؽ�һ��ѧ�����г�����������һ�濿ǽ�����ǽ�ij���Ϊ12�ף��ƻ����쳵������Ϊ80ƽ��������֪���е�ľ����Ͽ�ʹ�½���ǽ���ܳ�Ϊ26�ף�
(1)Ϊ�˷���ѧ��������ѧУ��������ǽƽ�е�һ�濪һ��2����������ô�������ij��Ϳ��ֱ�ӦΪ�����ף�
(2)��ͼ��Ϊ�˷���ѧ��ȡ����ʩ����λ�����ڳ������������ȿ���С·��ʹ��ͣ�����г������Ϊ54ƽ��������ôС·�Ŀ����Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������⣺�ٶԶ�����ȣ�����a��b��b��c����a��c������ͬһƽ���ڣ���a��b��b��c����a��c����ac��bc����a��b��������ȷ���У�������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��ABCD��BC�ߵ��е㣬����AE���ӳ�AE��DC���ӳ����ڵ�F������AC��BF����EF=EC�����ж��ı���ABFC��ʲô�ı��Σ���֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB ![]() ����AB��CD֮��ȡһ��E������EA��EC����̽��
����AB��CD֮��ȡһ��E������EA��EC����̽��![]() AEC��
AEC��![]() EAB��
EAB��![]() ECD֮��Ĺ�ϵ
ECD֮��Ĺ�ϵ![]() ����Eȡ��AC��
����Eȡ��AC��![]() ��ͼ
��ͼ![]() ����
����![]() AEC
AEC![]() ���ɴ˿ɵ�
���ɴ˿ɵ�![]() AEC
AEC![]() EAB
EAB![]() ECD��
ECD��![]() AEC
AEC![]() EAB
EAB![]() ECD
ECD![]() �����Eȡ��AC������
�����Eȡ��AC������![]() ��ͼ
��ͼ![]() �����ۻ���ʲô��
�����ۻ���ʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������λ�ڶ����غ����й���½�������жΣ�½�������ԼΪ9816ƽ���������9816�ÿ�ѧ��������ʾΪ��������
A.918.6��10B.91.86��102C.9.186��103D.0.9186��104
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx+b��������y=ax2��a��0���ཻ��A��B���㣨��A�ڵ�B����ࣩ����y���������ཻ�ڵ�C������A��AD��x�ᣬ����ΪD��
��1������AOB=60����AB��x�ᣬAB=2����a��ֵ��
��2������AOB=90�㣬��A�ĺ�����Ϊ��4��AC=4BC�����B�����ꣻ
��3���ӳ�AD��BO�ཻ�ڵ�E����֤��DE=CO��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
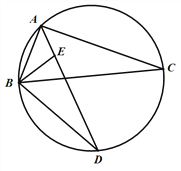
����Ŀ����ͼ�� ![]() ��ƽ���߽�
��ƽ���߽�![]() �����Բ�ڵ�
�����Բ�ڵ�![]() ��
�� ![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ��
��
��1����֤�� ![]() ��
��
��2����![]() ��
�� ![]() ����
����![]() ���Բ�İ뾶��
���Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڽ�����Ļ��㳡�����ϣ�����������㳡����IJ��ϣ�һ���dz�Ϊ![]() cm����Ϊ
cm����Ϊ![]() cm�ij����ΰ�ģ���ͼ������һ���DZ߳�Ϊ
cm�ij����ΰ�ģ���ͼ������һ���DZ߳�Ϊ![]() cm�������ε�ש����ͼ�ڣ�
cm�������ε�ש����ͼ�ڣ�

��1���ü�����ͼ����ʾ�������ε�ש��ƴ��һ���µ������Σ���д���������ε����
��д��һ�����������Ĵ𰸼��ɣ���
��2�������ڷ������ijЩ��ѧ����ʱ������Ҫ�Ƚ������������ʽ�Ĵ�С���������
��IJ���һ��Ҫ����һ����ת�������С���������dz��õķ���֮һ����ν������
����������ͨ��������Σ������ò�ķ�����ȷ�����ǵĴ�С����Ҫ�Ƚϴ���ʽM��
N�Ĵ�С��ֻҪ�������ǵIJ�![]() ����
����![]() ����
����![]() ����
����![]() ����
����
![]() ����
����![]() ����
����![]() ��
��
�����á����������������⣺����ͼ����ʾ���Ŀ鳤���ΰ���̳���ͼ�۵Ĵ������λ���ͼ�ܵĴ��Σ��м�ֱ�ճ�һ��С�����κ�С�����Σ�ͼ����Ӱ���֣���
�� ���ú�![]() ��
��![]() �Ĵ���ʽ�ֱ��ʾͼ�ۺ�ͼ������Ӱ���ֵ������
�Ĵ���ʽ�ֱ��ʾͼ�ۺ�ͼ������Ӱ���ֵ������
�� �ԱȽ�ͼ�ۺ�ͼ������Ӱ���ֵ�����ĸ�����٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com