
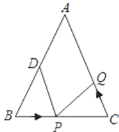
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1s后,BP= cm,CQ= cm.
(2)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(4)若点Q以(3)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次相遇?
【答案】(1)BP=3cm,CQ=3cm;(2)全等,理由详见解析;(3)![]() ;(4)经过
;(4)经过![]() s点P与点Q第一次相遇.
s点P与点Q第一次相遇.
【解析】
(1)速度和时间相乘可得BP、CQ的长;
(2)利用SAS可证三角形全等;
(3)三角形全等,则可得出BP=PC,CQ=BD,从而求出t的值;
(4)第一次相遇,即点Q第一次追上点P,即点Q的运动的路程比点P运动的路程多10+10=20cm的长度.
解:(1)BP=3×1=3㎝,
CQ=3×1=3㎝
(2)∵t=1s,点Q的运动速度与点P的运动速度相等
∴BP=CQ=3×1=3cm,
∵AB=10cm,点D为AB的中点,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,
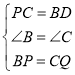
∴△BPD≌△CQP(SAS)
(3)∵点Q的运动速度与点P的运动速度不相等,
∴BP与CQ不是对应边,
即BP≠CQ
∴若△BPD≌△CPQ,且∠B=∠C,
则BP=PC=4cm,CQ=BD=5cm,
∴点P,点Q运动的时间t=![]() s,
s,
∴![]() cm/s;
cm/s;
(4)设经过x秒后点P与点Q第一次相遇.
由题意,得![]() x=3x+2×10,
x=3x+2×10,
解得![]()
∴经过![]() s点P与点Q第一次相遇.
s点P与点Q第一次相遇.


科目:初中数学 来源: 题型:
【题目】如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线![]() (x<0)分别交于点C(-1,2)、D(a,1).
(x<0)分别交于点C(-1,2)、D(a,1).
(1)分别求出直线及双曲线的解析式;
(2)利用图象直接写出,当x在什么范围内取值时,y1>y2.
(3)请把直线![]() 上y1<y2时的部分用黑色笔描粗一些.
上y1<y2时的部分用黑色笔描粗一些.
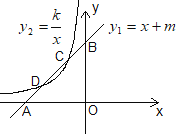
查看答案和解析>>
科目:初中数学 来源: 题型:
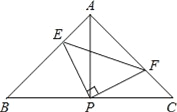
【题目】如图已知在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB和AC于点E、F,给出以下五个结论正确的个数有( )
①AE=CF②∠APE=∠CPF ③△BEP≌△AFP④△EPF是等腰直角三角形⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),S四边形AEPF=![]() S△ABC.
S△ABC.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形![]() ,
,![]() ,点
,点![]() 在直线
在直线![]() 上运动(点
上运动(点![]() 和点
和点![]() ,
,![]() 不重合,点
不重合,点![]() ,
,![]() ,
,![]() 不在同一条直线上),若记
不在同一条直线上),若记![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() .
.
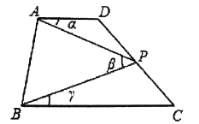
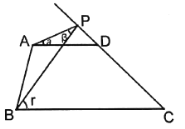
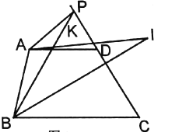
图1 图2 图3
(1)如图1,当点![]() 在线段
在线段![]() 上运动时,写出
上运动时,写出![]() ,
,![]() ,
,![]() 之间的关系,并说出理由;
之间的关系,并说出理由;
(2)如图2,如果点![]() 在线段
在线段![]() 的延长线上运动,探究
的延长线上运动,探究![]() ,
,![]() ,
,![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
(3)如图3,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:
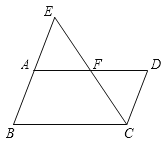
(1)∵EB∥DC, (已知)
∴∠DAE=∠__. ( ___________________________________)
(2)∵∠BCF+∠AFC=180°,(已知)
∴ ____∥___. ( ___________________________________)
(3)∵ ____∥___, (已知)
∴∠EFA=∠ECB . ( ___________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() 分)如图,管中放置着三根同样的绳子
分)如图,管中放置着三根同样的绳子![]() ,
, ![]() ,
, ![]() .
.
(![]() )小明从
)小明从![]() 这三根绳子中随机选一根,恰好选中绳子
这三根绳子中随机选一根,恰好选中绳子![]() 的概率是__________.
的概率是__________.
(![]() )小明先从左端
)小明先从左端![]() ,
, ![]() ,
, ![]() 三个绳头中随机选两个打一个结,再从右端
三个绳头中随机选两个打一个结,再从右端![]() ,
, ![]() ,
, ![]() 三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() 分)如图,管中放置着三根同样的绳子
分)如图,管中放置着三根同样的绳子![]() ,
, ![]() ,
, ![]() .
.
(![]() )小明从
)小明从![]() 这三根绳子中随机选一根,恰好选中绳子
这三根绳子中随机选一根,恰好选中绳子![]() 的概率是__________.
的概率是__________.
(![]() )小明先从左端
)小明先从左端![]() ,
, ![]() ,
, ![]() 三个绳头中随机选两个打一个结,再从右端
三个绳头中随机选两个打一个结,再从右端![]() ,
, ![]() ,
, ![]() 三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
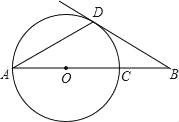
【题目】如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
(1)求证:BD是⊙O的切线;
(2)求CB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com