练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
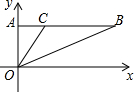
    12．如图，在平面直角坐标系中，△OAB的顶点A、B的坐标分别为（0，1）、（2，1），点C在边AB上（不与点B重合），设点C的横坐标为m，△BOC的面积为S，则下面能够反映S与m之间的函数关系的图象是（　　）
    A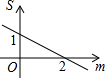．B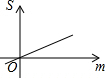．C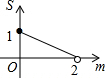．D．

    分析 根据函数图象可知OA=2，BC=2-m，从而可以表示出三角形BOC的面积，从而可以得到S与m之间的函数图象，且0≤m＜2．

    解答 解：由题意可得，${S}_{△BOC}=\frac{BC×OA}{2}=\frac{（2-m）×2}{2}$=2-m，
    所以，S随着m的增大而减小，当m=0时，取得最大值2，m的取值范围是0≤m＜2，
    故选C．

    点评 本题考查动点问题的函数图象，解题的关键是明确题意，可以表示出三角形的面积关系式，利用数形结合的思想解答问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．2015年我市人均GDP约为34800元，34800用科学记数法表示为3.48×104．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．计算（-2a）2的结果是（　　）
    A．-4a2B．2a2C．-2a2D．4a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．长春市轻轨3号线开通以来，极大缓解了城市的交通压力，据统计，每天轻轨的运载人数为16600人次，16600这个数用科学记数法表示为（　　）
    A．16.6×103B．1.66×104C．166×102D．1.66×105

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．甲、乙两车从A地驶向B地，甲车比乙车早行驶2h，并且在途中休息了0.5h，休息前后速度相同，如图是甲、乙两车行驶的距离y（km）与时间x（h）的函数图象．
    （1）图中a=40．
    （2）求出甲车行驶路程y（km）与时间x（h）之间的函数关系式．
    （3）当两车恰好相距50km时，直接写出甲车行驶的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．感知：如图①，在矩形ABCD中，点E是边BC的中点，将△ABE沿AE折叠，使点B落在矩形ABCD内部的点F处，延长AF交CD于点G，连结FC，易证∠GCF=∠GFC．
    探究：将图①中的矩形ABCD改为平行四边形，其他条件不变，如图②，判断∠GCF=∠GFC是否仍然相等，并说明理由．
    应用：如图②，若AB=5，BC=6，则△ADG的周长为16．

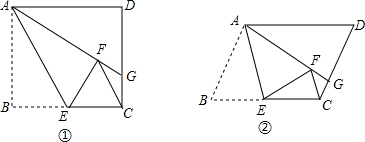
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

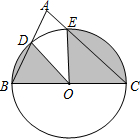    4．如图，以BC为直径的半圆⊙O与△ABC的边AB、AC分别相交于点D、E．若∠A=80°，BC=4，则图中阴影部分图形的面积和为（　　）
    A．$\frac{64}{9}π$B．$\frac{32}{9}π$C．$\frac{16}{9}π$D．$\frac{8}{9}π$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE，交AC于点F．
    （1）如图1，当DE平分∠CDB时，求证：AD=AF．
    （2）如图1，当DE平分∠CDB，且OF=1时，求正方形ABCD的边长．
    （3）如图2，当E是BC的中点时，过点F作FG⊥BC于点G，求证：CG=$\frac{1}{2}$BG．

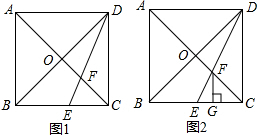
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．
    【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．
    【类比引申】
    如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足∠BAD=2∠EAF关系时，仍有EF=BE+FD．
    【探究应用】
    如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=（40$\sqrt{3}$-40）米，现要在E、F之间修一条笔直道路，求这条道路EF的长为40（$\sqrt{3}$+1）米．

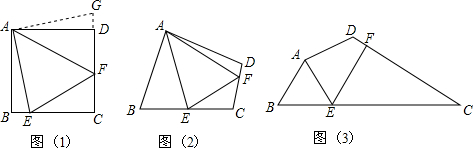
    查看答案和解析>>

    同步练习册答案