
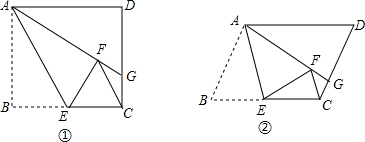
分析 探究:由?ABCD及折叠可得∠B+∠ECG=∠AFE+∠ECG=∠AFE+∠EFG=180°,即∠ECG=∠EFG,再根据EB=EF=EC得∠EFC=ECF,从而可得∠GCF=∠GFC;
应用:由(1)中∠GCF=∠GFC得GF=GC,AF=AB,根据△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD可得.
解答 解:探究:∠GCF=∠GFC,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠ECG=180°,
又∵△AFE是由△ABE翻折得到,
∴∠AFE=∠B,EF=BE,
又∵∠AFE+∠EFG=180°,
∴∠ECG=∠EFG,
又∵点E是边BC的中点,
∴EC=BE,
∵EF=BE,
∴EC=EF,
∴∠ECF=∠EFC,
∴∠ECG-∠ECF=∠EFG-∠EFC,
∴∠GCF=∠GFC;
应用:∵△AFE是由△ABE翻折得到,
∴AF=AB=5,
由(1)知∠GCF=∠GFC,
∴GF=GC,
∴△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD=AD+AB+CD=6+5+5=16,
故答案为:应用、16.
点评 该题主要考查了翻折变换的性质、平行四边形的性质等几何知识点及其应用问题,解题的关键是牢固掌握翻折变换的性质、平行四边形的性质等几何知识点.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
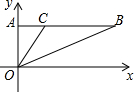 如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(0,1)、(2,1),点C在边AB上(不与点B重合),设点C的横坐标为m,△BOC的面积为S,则下面能够反映S与m之间的函数关系的图象是( )
如图,在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(0,1)、(2,1),点C在边AB上(不与点B重合),设点C的横坐标为m,△BOC的面积为S,则下面能够反映S与m之间的函数关系的图象是( )| A. | 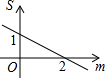 | B. | 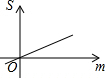 | C. | 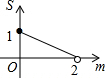 | D. | 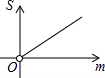 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
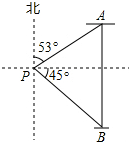 如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)
如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
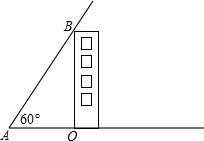 请从以下两个小题中个任意选一作答,若对选,则按第一题计分.
请从以下两个小题中个任意选一作答,若对选,则按第一题计分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com