
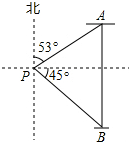 如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)
如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)科目:初中数学 来源: 题型:填空题
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:
某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:| 组别 | 预习时间x(分钟) | 频数 |
| 1 | 0≤x<5 | 8 |
| 2 | 5≤x<10 | m |
| 3 | 10≤x<15 | 18 |
| 4 | 15≤x<20 | 13 |
| 合计 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -ab+1 | B. | -ab+b | C. | -a+1 | D. | -a-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
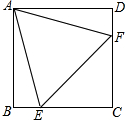 如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.
如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com