
【题目】如图,点E到△ABC三边的距离相等,过点E作MN∥BC交AB于M,交AC于N.若BM+CN=2019,则线段NM的长为( )
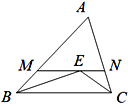
A.2017B.2018C.2019D.2020
科目:初中数学 来源: 题型:
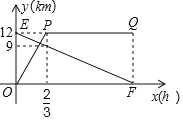
【题目】甲骑自行车从![]() 地出发前往
地出发前往![]() 地,同时乙步行从
地,同时乙步行从![]() 地出发前往
地出发前往![]() 地,如图的折线
地,如图的折线![]() 和线段
和线段![]() ,分别表示甲、乙两人与
,分别表示甲、乙两人与![]() 地的距离
地的距离![]() 甲 ,
甲 ,![]() 乙与他们所行时间
乙与他们所行时间![]() 之间的函数关系.
之间的函数关系.
(1)求线段![]() 对应的
对应的![]() 甲与
甲与![]() 的函数关系式并注明自变量
的函数关系式并注明自变量![]() 的取值范围;
的取值范围;
(2)求![]() 乙与
乙与![]() 的函数关系式及乙到达
的函数关系式及乙到达![]() 地所用的时间;
地所用的时间;
(3)经过 小时,甲、乙两人相距![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:弦切角:顶点在圆上,一边与圆相交,另一边和圆相切的角叫弦切角.
问题情景:已知如图所示,直线![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() 为
为![]() 的一条弦,
的一条弦,![]() 为弧
为弧![]() 所对的圆周角.
所对的圆周角.
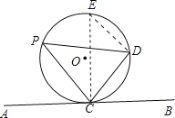
(1)猜想:弦切角![]() 与
与![]() 之间的关系.试用转化的思想:即连接
之间的关系.试用转化的思想:即连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,来论证你的猜想.
,来论证你的猜想.
(2)用自己的语言叙述你猜想得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
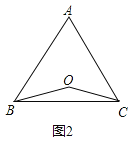
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,OE⊥AB,OF⊥AC,垂足分别为E,F.求证:AB=AC;

(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
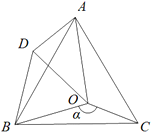
【题目】如图,点O是等边△ABC内一点,∠BOC=![]() ,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
(1) 求证:△BOD是等边三角形.
(2) 当![]() =150°时,试判断△AOD的形状,并说明理由.
=150°时,试判断△AOD的形状,并说明理由.
(3) 若△AOD是等腰三角形,请你直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC.
求作:平行四边形ABCD.
以下是甲、乙两同学的作业.
甲:
①以点C为圆心,AB长为半径作弧;
②以点A为圆心,BC长为半径作弧;
③两弧在BC上方交于点D,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图1)
乙:
①连接AC,作线段AC的垂直平分线,交AC于点M;
②连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图2)
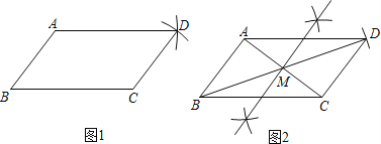
老师说甲、乙同学的作图都正确,你更喜欢______的作法,他的作图依据是:______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com