
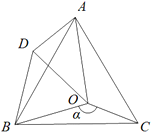
【题目】如图,点O是等边△ABC内一点,∠BOC=![]() ,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
,∠AOC=100°,将△BOC绕点B按逆时针方向旋转60°得到△BDA,连接OD.
(1) 求证:△BOD是等边三角形.
(2) 当![]() =150°时,试判断△AOD的形状,并说明理由.
=150°时,试判断△AOD的形状,并说明理由.
(3) 若△AOD是等腰三角形,请你直接写出![]() 的度数.
的度数.
【答案】(1)证明见解析;(2)α=150°时,△AOD是直角三角形;理由见解析;(3)130°或100°或160°
【解析】
(1)根据旋转的性质可得出OB=BD,∠OBD=60°,根据等边三角形的判定即可求证;
(2)由(1)的结论可得∠BDO=60°;由于α=150°,所以∠ADB=∠BOC=150°,继而可得∠ADO=∠ADB-∠ODB=90°,由∠AOC=100°,∠BOD=60°,可求出∠AOD=360°-∠α-∠AOC-∠COD=360°-150°-100°-60°=50°,根据三角形的内角即可判定三角形的形状;
(3)分AO=AD、AO=OD、DO=AD三种情况,根据等腰三角形的概念,三角形内角和定理计算.
(1)证明:∵将△BOC绕点B按逆时针方向旋转60°得△BDA,
∴BO=BD,∠OBD=60°,
∴△BOD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.理由是:
∵将△BOC绕点B按逆时针方向旋转60°得△BDA,
∴△BOC≌△BDA,
∴∠ADB=∠BOC=150°,
又∵△BOD是等边三角形,
∴∠ODB=60°,
∴∠ADO=∠ADB-∠ODB=90°,
∵∠α=150°,∠AOC=100°,∠BOD=60°,
∴∠AOD=360°-∠α-∠AOC-∠COD=360°-150°-100°-60°=50°,
∴△AOD不是等腰直角三角形,
即△AOD是直角三角形.
(3) ∵△BOD是等边三角形,
∴∠ADO=α-60°,
∵OD=OA,
∴∠OAD=∠ODA=α-60°,
∴∠AOD=180°-2(α-60°),解得α=100°;
当OD=AD时,α+100°+60°+∠AOD=360°,
∠AOD=![]() ,解得α=160°;
,解得α=160°;
当OA=AD时,α+100°+60°+∠AOD=360°,∠AOD=α-60°,解得,α=130°
综合可得:130°或100°或160°


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
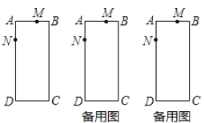
【题目】长方形![]() 中,
中,![]() ,点
,点![]() 和点
和点![]() 都是从
都是从![]() 点出发,点
点出发,点![]() 在这个长方形的边上顺时针运动,点
在这个长方形的边上顺时针运动,点![]() 在这个长方形的边上逆时针运动,它们的速度都是每秒1个单位,设它们的运动时间是
在这个长方形的边上逆时针运动,它们的速度都是每秒1个单位,设它们的运动时间是![]() 秒
秒![]()
(1)![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)在![]() 运动过程中,连接
运动过程中,连接![]() ,设线段
,设线段![]() 和点
和点![]() 所经过的路线所组成的封闭的图形面积是
所经过的路线所组成的封闭的图形面积是![]() ,求出
,求出![]() 与
与![]() 的函数关系式,并注明
的函数关系式,并注明![]() 的取值范围.
的取值范围.
(3)在上一问中,是否存在某个时刻![]() ,使得
,使得![]() 是长方形
是长方形![]() 面积的一半?若存在,求出
面积的一半?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
(4)当![]() 点在
点在![]() 上运动时(不包括点
上运动时(不包括点![]() ),存不存在某一时刻
),存不存在某一时刻![]() ,使得
,使得![]() 是直角三角形吗?若存在,求出
是直角三角形吗?若存在,求出![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E到△ABC三边的距离相等,过点E作MN∥BC交AB于M,交AC于N.若BM+CN=2019,则线段NM的长为( )
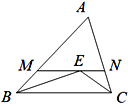
A.2017B.2018C.2019D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
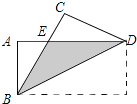
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法:①![]() 是等腰三角形,
是等腰三角形,![]() ;②折叠后
;②折叠后![]() 和
和![]() 一定相等;③折叠后得到的图形是轴对称图形;④
一定相等;③折叠后得到的图形是轴对称图形;④![]() 和
和![]() 一定是全等三角形.正确的是______(填序号).
一定是全等三角形.正确的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N.AH⊥MN于点H.
(1)当∠MAN绕点A旋转到BM=DN时,请你直接写出线段AH与AB的数量关系______.(不需证明)
(2)当∠MAN绕点A旋转到BM≠DN时,问(1)中线段AH与AB的数量关系还成立吗?若成立,给出证明,若不成立,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
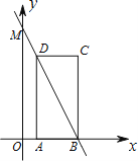
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(![]() ,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com