
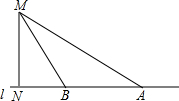
 如图,高速公路旁有一个测速站M到公路l的距离MN为60米,一辆小汽车在公路l上行驶,测得此车从点A行驶到点B所有的时间为3秒,已知∠MAN=30°,∠MBN=60°.
如图,高速公路旁有一个测速站M到公路l的距离MN为60米,一辆小汽车在公路l上行驶,测得此车从点A行驶到点B所有的时间为3秒,已知∠MAN=30°,∠MBN=60°.分析 (1)根据题意需求AB长.由已知易知AB=BM,解直角三角形MNB求出BM即AB,再求速度;
(2)利用(1)中所求,与限制速度比较得结论.
解答 解:(1)在Rt△AMN中,tan30°=$\frac{MN}{AN}$,则AN=$\frac{MN}{tan30°}$=60$\sqrt{3}$.
在Rt△BMN中,BN=MN×tan∠BMN=MN×tan30°=60×$\frac{\sqrt{3}}{3}$.
∴AB=AN-BN=60$\sqrt{3}$-20$\sqrt{3}$=40$\sqrt{3}$(m).
则A到B的平均速度为:$\frac{AB}{3}$=$\frac{40\sqrt{3}}{3}$(米/秒)≈23(米/秒),
答:此车从A到B的平均速度为每秒23米;
(2)由题意可得:80千米/时=$\frac{200}{9}$米/秒≈22米/秒<23米/秒.
答:此车已经超过限速.
点评 此题主要考查了勾股定理的应用,将已知条件和所求结论转化到同一个直角三角形中求解是解直角三角形的常规思路.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 25;25 | B. | 29;25 | C. | 27;25 | D. | 28;25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 两条对角线相等且相互平分的四边形是矩形 | |
| C. | 三点确定一个圆 | |
| D. | 相等的圆周角所对的弧相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com