
已知:关于x的方程mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值;
(3)在(2)的条件下,令y=mx2+(3m+1)x+3,如果当x1=a与x2=a+n(n≠0)时有y1=y2,求代数式4a2+12an+5n2+16n+8的值.
(1)证明见解析;
(2)m=1;
(3)4a2+12an+5n2+16n+8=24.
【解析】
试题分析:(1)分类讨论:当m=0时,原方程化为x+3=0,解得x=﹣3;当m≠0时,计算判别式得△=(3m﹣1)2,由于(3m﹣1)2≥0,则不论m为任何实数时总有两个实数根,所以不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根;
(2)先解方程mx2+(3m+1)x+3=0得到x1=﹣3,x2=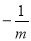 ,由于方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,易得m=1;
,由于方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,易得m=1;
(3)当m=1时得到y=x2+4x+3,当x1=a时,y1=a2+4a+3,当x2=a+n时,y2=(a+n)2+4(a+n)+3,则a2+4a+3=(a+n)2+4(a+n)+3,变形得 n(2a+n+4)=0,由于n≠0,所以2a=﹣n﹣4,然后变形4a2+12an+5n2+16n+8得到(2a)2+2a•6n+5n2+16n+8,再利用整体代入的方法计算.
试题解析:(1)当m=0时,原方程化为x+3=0,此时方程有实数根 x=﹣3;
当m≠0时,
∵△=(3m+1)2﹣12m=9m2﹣6m+1=(3m﹣1)2.
∵(3m﹣1)2≥0,
∴不论m为任何实数时总有两个实数根,
综上所述,不论m为任何实数时,方程 mx2+(3m+1)x+3=0总有实数根;
(2)当m≠0时,解方程mx2+(3m+1)x+3=0得 x1=﹣3,x2=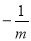 ,
,
∵方程mx2+(3m+1)x+3=0有两个不同的整数根,且m为正整数,
∴m=1;
(3)∵m=1,y=mx2+(3m+1)x+3,
∴y=x2+4x+3,
又∵当x1=a与x2=a+n(n≠0)时有y1=y2,
∴当x1=a时,y1=a2+4a+3,
当x2=a+n时,y2=(a+n)2+4(a+n)+3,
∴a2+4a+3=(a+n)2+4(a+n)+3,
化简得 2an+n2+4n=0,
即 n(2a+n+4)=0,
又∵n≠0,
∴2a=﹣n﹣4,
∴4a2+12an+5n2+16n+8
=(2a)2+2a•6n+5n2+16n+8
=(n+4)2+6n(﹣n﹣4)+5n2+16n+8
=24.
考点:1、根的判别式;2、根与系数的关系;3、整体思想


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源:2015届天津市河西区八年级下学期期末考试数学试卷(解析版) 题型:填空题
若以A(﹣0.5,0),B(2,O),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在第 _________ 象限.
查看答案和解析>>
科目:初中数学 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:解答题
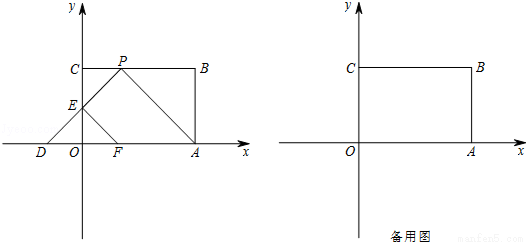
如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:选择题
点P(﹣1,2)关于y轴对称点的坐标是( )
A.(1,2) B.(﹣1,﹣2) C.(1,﹣2) D.(2,﹣1)
查看答案和解析>>
科目:初中数学 来源:2015届北京市门头沟区八年级下学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)如果BC+DF=9,CF=3,求正方形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源:2015届北京市门头沟区八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,并分别找出它们的中点M和N.如果测得MN=15m,则A,B两点间的距离为 m.

查看答案和解析>>
科目:初中数学 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:解答题
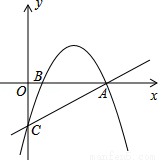
已知直线y=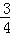 x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣
x﹣3与x轴交于点A,与y轴交于点C,抛物线y=﹣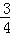 x2+mx+n经过点A和点C.
x2+mx+n经过点A和点C.
(1)求此抛物线的解析式;
(2)在直线CA上方的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:选择题
 ABCD中, ∠A比∠B小200,则∠A的度数为( )
ABCD中, ∠A比∠B小200,则∠A的度数为( )
A. 600 B. 800 C. 1000 D. 1200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com