
如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.
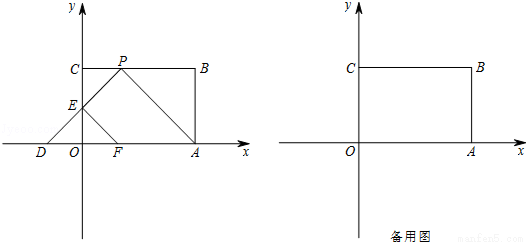
(1)P(1,2);(2)PE的解析式为:y=2x﹣2
【解析】
试题分析:(1)由等腰直角三角形的性质可知∠PAD=∠PDA=45°,再由矩形的性质求得∠1=∠2=45°,进而求得AB=BP=2即可求得.
(2)根据平行四边形的性质得出PD=DE,根据矩形的性质以及已知条件求得PD=PA,进而求得DM=AM,然后通过得出△PDM≌△EDO得出OD=DM=MA=1,EO=PM=2,即可求得.
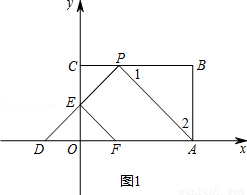
试题解析:(1)如图1,∵△APD为等腰直角三角形,∴∠APD=90°,
∴∠PAD=∠PDA=45°,
又∵四边形ABCD是矩形,
∴OA∥BC,∠B=90°,AB=OC,
∴∠1=∠2=45°,
∴AB=BP,
又∵OA=3,OC=2,
∴BP=2,CP=1,
∴P(1,2),
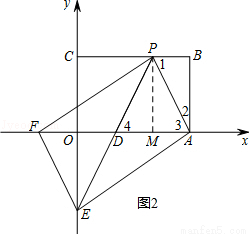
(2)如图2∵四边形APFE是平行四边形,
∴PD=DE,
∵OA∥BC,
∴∠CPD=∠4,∠1=∠3,
∵∠CPD=∠1,
∴∠3=∠4,
∴PD=PA,
过P作PM⊥x轴于M,
∴DM=MA,
又∵∠PDM=∠EDO,∠PMD=∠EOD=90°,
在△PDM与△EDO中,
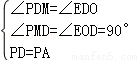 ,
,
∴△PDM≌△EDO(AAS),
∴OD=DM=MA=1,EO=PM=2,
∴P(2,2),E(0,﹣2),
∴PE的解析式为:y=2x﹣2;
考点:一次函数综合题


科目:初中数学 来源:2015届安徽省铜陵市八年级下学期期末考试数学试卷(解析版) 题型:解答题
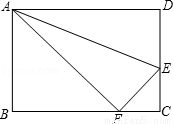
如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?用你学过的方法进行解释.
查看答案和解析>>
科目:初中数学 来源:2015届四川省成都市武侯区八年级下学期期末考试数学试卷(解析版) 题型:选择题
已知一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.8 B.6 C.5 D.3
查看答案和解析>>
科目:初中数学 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:解答题
某村计划建造了如图所示的矩形蔬菜温室,温室的长是宽的4倍,左侧是3米宽的空地,其它三侧各有1米宽的通道,矩形蔬菜种植区域的面积为288平方米.求温室的长与宽各为多少米?

查看答案和解析>>
科目:初中数学 来源:2015届北京市门头沟区八年级下学期期末考试数学试卷(解析版) 题型:解答题
已知:关于x的方程mx2+(3m+1)x+3=0.
(1)求证:不论m为任何实数,此方程总有实数根;
(2)如果该方程有两个不同的整数根,且m为正整数,求m的值;
(3)在(2)的条件下,令y=mx2+(3m+1)x+3,如果当x1=a与x2=a+n(n≠0)时有y1=y2,求代数式4a2+12an+5n2+16n+8的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com