
 如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM.
如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM.分析 (1)连接OA,只需证△OAN≌△OBM即可迅速得出结论;
(2)取NM中点D,连接OD、AD,则根据(1)中结论可知MN=OD+AD,而OD+AD≥OA,即OA就是MN的最小值.
解答 解:(1)△OMN是等腰直角三角形.
理由:连接OA,如图1,
∵在△ABC中,∠A=90°,AB=AC,O是BC的中点,
∴AO=BO=CO,∠B=∠C=45°;
在△OAN和OBM中,
$\left\{\begin{array}{l}{AO=BO}\\{∠NAO=∠B}\\{AN=BM}\end{array}\right.$,
∴△OAN≌△OBM(SAS),
∴ON=OM,∠AON=∠BOM;
又∵∠BOM+∠AOM=90°,
∴∠NOM=∠AON+∠AOM=90°,
∴△OMN是等腰直角三角形;
(2)取MN的中点D,连接OD,AD,如图2,
∵∠MON=∠NAM=90°,
∴OD=OA=$\frac{1}{2}$MN,
∴MN=OD+AD,
∵OD+AD≥AO,
∴MN≥AO,
∴MN的最小值为AO,
∵BC=2$\sqrt{2}$,
∴AO=$\sqrt{2}$,
∴MN的最小值为$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质、直角三角形斜边中线定理、三角形三边关系等知识点,难度适中.“中点”是本题的题眼,在初中阶段,与“中点”的几何知识并不多,同学们可自行总结一下“中点”有限几种用法,今后再遇到与“中点”有关的几何题目,就会反应迅速,作出辅助线也就很容易.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
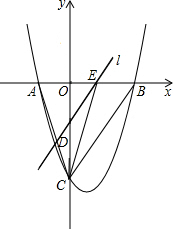 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向下、直线x=4、(4,5) | B. | 向下、直线x=-4、(-4,5) | ||
| C. | 向上、直线x=4、(4,5) | D. | 向上、直线x=-4、(-4,-5) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
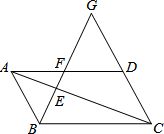 如图,在平行四边形ABCD中,点E是对角线AC上一点,且EC=2AE,连接BE并延长交AD于点F,交CD延长线于点G,则$\frac{BE}{EG}$=$\frac{1}{2}$.
如图,在平行四边形ABCD中,点E是对角线AC上一点,且EC=2AE,连接BE并延长交AD于点F,交CD延长线于点G,则$\frac{BE}{EG}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
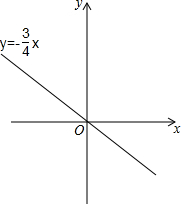 一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C.
一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C. 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com