
����Ŀ���ۺ���̽��
��ͼ��������y=��![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����B��C���㣬��M�ӵ�A������ÿ��1����λ���ȵ��ٶ����յ�B�˶�������CM�����߶�MC�Ƶ�M˳ʱ����ת90��õ��߶�MD������CD��BD�����M�˶���ʱ��Ϊt��t��0���������������⣺
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��ֱ��l����B��C���㣬��M�ӵ�A������ÿ��1����λ���ȵ��ٶ����յ�B�˶�������CM�����߶�MC�Ƶ�M˳ʱ����ת90��õ��߶�MD������CD��BD�����M�˶���ʱ��Ϊt��t��0���������������⣺
��1�����A��������ֱ��l�ı���ʽ��
��2����ֱ��д����D�����꣨�ú�t��ʽ�ӱ�ʾ���������D����ֱ��l��ʱ��t��ֵ��
�����M�˶��Ĺ������߶�CD���ȵ���Сֵ��
��3���ڵ�M�˶��Ĺ����У���ֱ��l���Ƿ���ڵ�P��ʹ�á�BDP�ǵȱ������Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��A����3��0����y=��![]() x+
x+![]() ����2����D��t��3+
����2����D��t��3+![]() ��t��3������CD��СֵΪ
��t��3������CD��СֵΪ![]() ����3��P��2����
����3��P��2����![]() �������ɼ�����.
�������ɼ�����.
��������
��1����y=0ʱ����![]() =0���ⷽ�����A��-3��0����B��1��0�����ɽ���ʽ��C��0��
=0���ⷽ�����A��-3��0����B��1��0�����ɽ���ʽ��C��0��![]() ��������ϵ��������ֱ��l�ı���ʽ��
��������ϵ��������ֱ��l�ı���ʽ��
��2���ֵ���M��AO���˶�ʱ������M��OB���˶�ʱ���������ۿ���D�����꣬��D���������ֱ�߽���ʽ���t��ֵ���߶�CD�ǵ���ֱ��������CMDб�ߣ���CD��С����CM��С�����ݹ��ɶ��������M�˶��Ĺ������߶�CD���ȵ���Сֵ��
��3���ֵ���M��AO���˶�ʱ����0��t��3ʱ������M��OB���˶�ʱ����3��t��4ʱ���������ۿ���P�����꣮
��1����y=0ʱ����![]() =0�����x1=1��x2=��3��
=0�����x1=1��x2=��3��
�ߵ�A�ڵ�B����࣬
��A����3��0����B��1��0����
�ɽ���ʽ��C��0��![]() ����
����
��ֱ��l�ı���ʽΪy=kx+b����B��C������������b=![]() mk��
mk��![]() ��
��
��ֱ��l�ı���ʽΪy=��![]() x+
x+![]() ��
��
��2������M��AO���˶�ʱ����ͼ��

�������֪AM=t��OM=3��t��MC��MD������D��x��Ĵ��ߴ���ΪN��
��DMN+��CMO=90�㣬��CMO+��MCO=90�㣬
���MCO=��DMN��
����MCO����DMN��
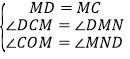 ��
��
���MCO�ա�DMN��
��MN=OC=![]() ��DN=OM=3��t��
��DN=OM=3��t��
��D��t��3+![]() ��t��3����
��t��3����
ͬ��������M��OB���˶�ʱ����ͼ��
OM=t��3����MCO�ա�DMN��MN=OC=![]() ��ON=t��3+
��ON=t��3+![]() ��DN=OM=t��3��
��DN=OM=t��3��
��D��t��3+![]() ��t��3����
��t��3����
���ϵã�D��t��3+![]() ��t��3����
��t��3����
��D���������ֱ�߽���ʽ��t=6��2![]() ��
��
�߶�CD�ǵ���ֱ��������CMDб�ߣ���CD��С����CM��С��
��M��AB���˶���
�൱CM��ABʱ��CM��̣�CD��̣���CM=CO=![]() �����ݹ��ɶ�����CD��С
�����ݹ��ɶ�����CD��С![]() ��
��
��3������M��AO���˶�ʱ����ͼ����0��t��3ʱ��

��tan��CBO=![]() =
=![]() ��
��
���CBO=60�㣬
�ߡ�BDP�ǵȱ������Σ�
���DBP=��BDP=60�㣬BD=BP��
���NBD=60�㣬DN=3��t��AN=t+![]() ��NB=4��t��
��NB=4��t��![]() ��tan��NBO=
��tan��NBO=![]() ��
��
![]() =
=![]() �����t=3��
�����t=3��![]() ��
��
������t=3��![]() �Ǵ˷��̵Ľ⣬
�Ǵ˷��̵Ľ⣬
����P��x��Ĵ��߽��ڵ�Q����֪��PQB�ա�DNB��
��BQ=BN=4��t��![]() =1��PQ=
=1��PQ=![]() ��OQ=2��P��2����
��OQ=2��P��2����![]() ����
����
ͬ��������M��OB���˶�ʱ����3��t��4ʱ��
�ߡ�BDP�ǵȱ������Σ�
���DBP=��BDP=60�㣬BD=BP��
���NBD=60�㣬DN=t��3��NB=t��3+![]() ��1=t��4+
��1=t��4+![]() ��tan��NBD=
��tan��NBD=![]() ��
��
![]() =
=![]() �����t=3��
�����t=3��![]() ��
��
������t=3��![]() �Ǵ˷��̵Ľ⣬t=3��
�Ǵ˷��̵Ľ⣬t=3��![]() �����������⣬�ᣩ��
�����������⣬�ᣩ��
��P��2����![]() ����
����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���εı߳���һ���Խ��ߵij���Ϊ2 cm�������ε����Ϊ( )
A. 3cm2 B. 4 cm2 C. ![]() cm2 D. 2
cm2 D. 2![]() cm2
cm2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ��AEƽ�֡�BAC����O�ڵ�E����BC�ڵ�D������E��ֱ��l��BC��

��1���ж�ֱ��l���O��λ�ù�ϵ����˵�����ɣ�
��2������ABC��ƽ����BF��AD�ڵ�F����֤��BE=EF��
��3���ڣ�2���������£���DE=4��DF=3����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
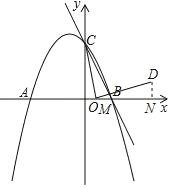
����Ŀ����Rt��ABC�У���ACB=90����AC=BC��DΪBC�е㣬CE��AD��E��BF��AC��CE���ӳ�����F��
��1����֤����ACD�ա�CBF��
��2����֤��AB��ֱƽ��DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Դ�����������ʻ��������ܾ��õ������ܵ���������֮�����ľ����������������ļ������ӣ���ǰ�г�������Ư�����Ӷ����Ϸִ��綯�ͻ�϶������֣�����;���ַ�Ϊ����ʽ������ʽ���֣����й�������ҵЭ���ṩ����Ϣ��2017��ȫ������Դ���ó����ۼ�����Ϊ57.9���������У����綯���ó�����Ϊ46.8��������϶������ó�����Ϊ11.1������ 2017��ȫ������Դ���ó����ۼ�����Ϊ19.8���������У����綯���ó�����Ϊ18.4��������϶������ó�����Ϊ1.4��������������ϲ��Ͻ���������⣺
��1������ͳ�Ʊ���ʾ�ҹ�2017������Դ������������������
��2��Сӱ����������Ϣ�������2017���ҹ�����Դ�����������Ϊ77.7����������������2017���ҹ�����Դ�������������������������ͳ��ͼ����ͼ1�����㽫��ͼ�������������еİٷ�����ȷ��0.1%����
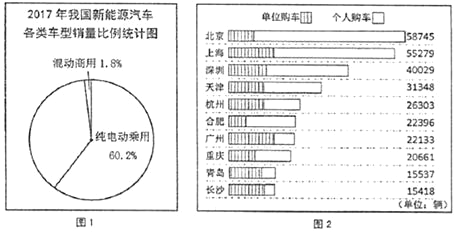
��3��2017���ҹ�����Դ���ó�������ߵ�ʮ���������������ͼ2�������ͼ2����Ϣд����Щ��������Դ���ó�����������ص㣨д��һ�����ɣ���
��4��������ʾ��2018��1��3�µ�����Դ���ó����������а���λ��ǰ�ĵij����DZ��ǵϡ������������������μ����ʵ���Ĵ�ѧ��С����������������ҽ���������У������ĸ���ȫ��ͬ��ƹ������б�ţ�����1��2��3��4�����ζ�Ӧ�����ĸ����ң�������ƹ������벻���Ĵ����н��ȣ�����һ���ó�����ƹ������ƹ�����ϵı�ž���Ҫ���еij��ң���С��ǡ�õ��������ǵ����������������������ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=mx2+��6��2m��x+m��3��ͼ����ͼ��ʾ����m��ȡֵ��Χ�ǣ�������
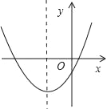
A. m��3 B. m��3 C. 0��m��3 D. 0��m��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������µ�������y��a(x��1)(x��9)��x�ύ��A��B���㣬��y�ύ�ڵ�C������ACB��90������a��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽��Ӧ�ã�
��1�����㣺![]() ___________��
___________��![]() ______________��
______________��
��2������ij˷��������ܼ�࣬�㷢����ʲô���ɣ���ʽ�����ú���ĸ![]() �ĵ�ʽ��ʾ�ù�ʽΪ��_______________��
�ĵ�ʽ��ʾ�ù�ʽΪ��_______________��
��3�����и�ʽ���õڣ�2����Ĺ�ʽ������ǣ� ��
A��![]() B��
B��![]()
C��![]() D��
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�һ����Ʒ�Ľ���Ϊÿ��30Ԫ���ۼ�Ϊÿ��40Ԫ��ÿ���������48����Ϊ������ٿ�棬�̳��������۴�����
��1��������Ʒ���������µ���ͬ�İٷ��ʺ��ۼ۽���ÿ��32.4Ԫ���������½��İٷ��ʣ�
��2�������飬��ÿ����0.5Ԫ��ÿ��ɶ�����4������ôÿ��Ҫ����510Ԫ������ÿ��Ӧ���۶���Ԫ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com