
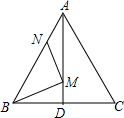
 如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是
如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是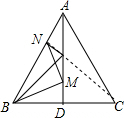 解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,
解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,| 1 |
| 2 |
| BC2-BN2 |
| 62-32 |
| 3 |
| 3 |
| 3 |


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
 如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.
如图所示,在O点的观测站测得渔船A、B的方向分别为北偏东45°,南偏西30°,为了减少相互干扰并取得较好的捕鱼效益,渔船C恰好位于∠AOB的平分线上,求渔船C相对观测站的方向.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、和为180°的两个角互为邻补角 |
| B、有公共顶点且互补的两个角互为邻补角 |
| C、有一条公共边且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
| D、有公共顶点且有一条公共边,另一边互为反向延长线的两个角互为邻补角 |
查看答案和解析>>
科目:初中数学 来源: 题型:
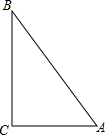 如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.
如图,点A表示小雨家,点B表示小樱家,点C表示小丽家,她们三家恰好组成一个直角三角形,其中AC⊥BC,AC=900米,BC=1200米,AB=1500米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com