
 P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.
P为等边△ABC内一点,PA=5,PB=4,PC=3,求∠BPC.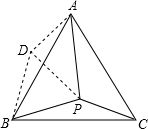 解:如图,将△BPC绕点B逆时针旋转60°得到△ABD,
解:如图,将△BPC绕点B逆时针旋转60°得到△ABD,

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
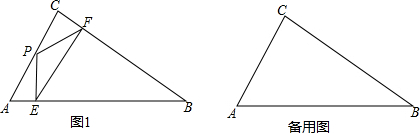
查看答案和解析>>
科目:初中数学 来源: 题型:
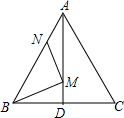 如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是
如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是查看答案和解析>>
科目:初中数学 来源: 题型:
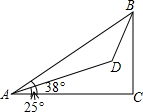 某勘测队在山脚测得山顶的仰角为38°,沿倾斜角为25°的山坡前进800米后,又测得山顶的仰角为62°,求山的高度(精确到0.1米).(cos13°=0.9744,sin13°=0.2250,cot24°=2.246,sin38°=0.6157).
某勘测队在山脚测得山顶的仰角为38°,沿倾斜角为25°的山坡前进800米后,又测得山顶的仰角为62°,求山的高度(精确到0.1米).(cos13°=0.9744,sin13°=0.2250,cot24°=2.246,sin38°=0.6157).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com