
【题目】在平面直角坐标系中,已知抛物线y= ![]() x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.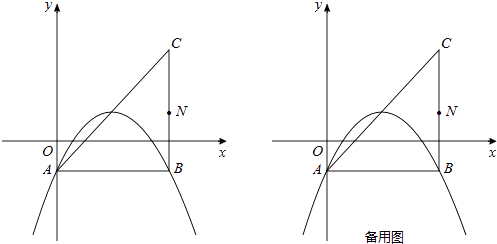
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究 ![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
【答案】
(1)
解:∵等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3)
∴点B的坐标为(4,﹣1).
∵抛物线过A(0,﹣1),B(4,﹣1)两点,
∴  ,解得:b=2,c=﹣1,
,解得:b=2,c=﹣1,
∴抛物线的函数表达式为:y= ![]() x2+2x﹣1
x2+2x﹣1
(2)
解:方法一:
i)∵A(0,﹣1),C(4,3),
∴直线AC的解析式为:y=x﹣1.
设平移前抛物线的顶点为P0,则由(1)可得P0的坐标为(2,1),且P0在直线AC上.
∵点P在直线AC上滑动,∴可设P的坐标为(m,m﹣1),
则平移后抛物线的函数表达式为:y= ![]() (x﹣m)2+m﹣1.
(x﹣m)2+m﹣1.
解方程组: 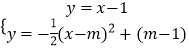 ,
,
解得 ![]() ,
, ![]()
∴P(m,m﹣1),Q(m﹣2,m﹣3).
过点P作PE∥x轴,过点Q作QF∥y轴,则
PE=m﹣(m﹣2)=2,QF=(m﹣1)﹣(m﹣3)=2.
∴PQ=2 ![]() =AP0.
=AP0.
若以M、P、Q三点为顶点的等腰直角三角形,则可分为以下两种情况:
① 当PQ为直角边时:点M到PQ的距离为2 ![]() (即为PQ的长).
(即为PQ的长).
由A(0,﹣1),B(4,﹣1),P0(2,1)可知,
△ABP0为等腰直角三角形,且BP0⊥AC,BP0=2 ![]() .
.
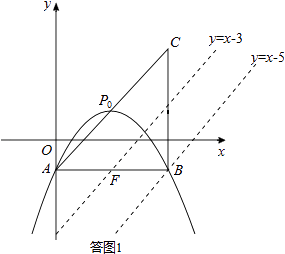
如答图1,过点B作直线l1∥AC,交抛物线y= ![]() x2+2x﹣1于点M,则M为符合条件的点.
x2+2x﹣1于点M,则M为符合条件的点.
∴可设直线l1的解析式为:y=x+b1,
∵B(4,﹣1),∴﹣1=4+b1,解得b1=﹣5,
∴直线l1的解析式为:y=x﹣5.
解方程组  ,得:
,得: ![]() ,
, ![]()
∴M1(4,﹣1),M2(﹣2,﹣7).
②当PQ为斜边时:MP=MQ=2,可求得点M到PQ的距离为 ![]() .
.
如答图2,取AB的中点F,则点F的坐标为(2,﹣1).
由A(0,﹣1),F(2,﹣1),P0(2,1)可知:
△AFP0为等腰直角三角形,且点F到直线AC的距离为 ![]() .
.
过点F作直线l2∥AC,交抛物线y= ![]() x2+2x﹣1于点M,则M为符合条件的点.
x2+2x﹣1于点M,则M为符合条件的点.
∴可设直线l2的解析式为:y=x+b2,
∵F(2,﹣1),∴﹣1=2+b2,解得b2=﹣3,
∴直线l2的解析式为:y=x﹣3.
解方程组  ,得:
,得: ![]() ,
, ![]()
∴M3(1+ ![]() ,﹣2+
,﹣2+ ![]() ),M4(1﹣
),M4(1﹣ ![]() ,﹣2﹣
,﹣2﹣ ![]() ).
).
综上所述,所有符合条件的点M的坐标为:
M1(4,﹣1),M2(﹣2,﹣7),M3(1+ ![]() ,﹣2+
,﹣2+ ![]() ),M4(1﹣
),M4(1﹣ ![]() ,﹣2﹣
,﹣2﹣ ![]() ).
).
方法二:
∵A(0,1),C(4,3),
∴lAC:y=x﹣1,
∵抛物线顶点P在直线AC上,设P(t,t﹣1),
∴抛物线表达式: ![]() ,
,
∴lAC与抛物线的交点Q(t﹣2,t﹣3),
∵一M、P、Q三点为顶点的三角形是等腰直角三角形,P(t,t﹣1),
①当M为直角顶点时,M(t,t﹣3), ![]() ,
,
∴t=1± ![]() ,
,
∴M1(1+ ![]() ,
, ![]() ﹣2),M2(1﹣
﹣2),M2(1﹣ ![]() ,﹣2﹣
,﹣2﹣ ![]() ),
),
②当Q为直角顶点时,点M可视为点P绕点Q顺时针旋转90°而成,
将点Q(t﹣2,t﹣3)平移至原点Q′(0,0),则点P平移后P′(2,2),
将点P′绕原点顺时针旋转90°,则点M′(2,﹣2),
将Q′(0,0)平移至点Q(t﹣2,t﹣3),则点M′平移后即为点M(t,t﹣5),
∴ ![]() ,
,
∴t1=4,t2=﹣2,
∴M1(4,﹣1),M2(﹣2,﹣7),
③当P为直角顶点时,同理可得M1(4,﹣1),M2(﹣2,﹣7),
综上所述,所有符合条件的点M的坐标为:
M1(4,﹣1),M2(﹣2,﹣7),M3(1+ ![]() ,﹣2+
,﹣2+ ![]() ),M4(1﹣
),M4(1﹣ ![]() ,﹣2﹣
,﹣2﹣ ![]() ).
).
ii) ![]() 存在最大值.理由如下:
存在最大值.理由如下:
由i)知PQ=2 ![]() 为定值,则当NP+BQ取最小值时,
为定值,则当NP+BQ取最小值时, ![]() 有最大值.
有最大值.

如答图2,取点B关于AC的对称点B′,易得点B′的坐标为(0,3),BQ=B′Q.
连接QF,FN,QB′,易得FN∥PQ,且FN=PQ,
∴四边形PQFN为平行四边形.
∴NP=FQ.
∴NP+BQ=FQ+B′Q≥FB′= ![]() =2
=2 ![]() .
.
∴当B′、Q、F三点共线时,NP+BQ最小,最小值为2 ![]() .
.
∴ ![]() 的最大值为
的最大值为 ![]() =
= ![]()
【解析】(1)先求出点B的坐标,然后利用待定系数法求出抛物线的函数表达式;(2)(i)首先求出直线AC的解析式和线段PQ的长度,作为后续计算的基础.
若△MPQ为等腰直角三角形,则可分为以下两种情况:①当PQ为直角边时:点M到PQ的距离为2 ![]() .此时,将直线AC向右平移4个单位后所得直线(y=x﹣5)与抛物线的交点,即为所求之M点;②当PQ为斜边时:点M到PQ的距离为
.此时,将直线AC向右平移4个单位后所得直线(y=x﹣5)与抛物线的交点,即为所求之M点;②当PQ为斜边时:点M到PQ的距离为 ![]() .此时,将直线AC向右平移2个单位后所得直线(y=x﹣3)与抛物线的交点,即为所求之M点.(ii)由(i)可知,PQ=2
.此时,将直线AC向右平移2个单位后所得直线(y=x﹣3)与抛物线的交点,即为所求之M点.(ii)由(i)可知,PQ=2 ![]() 为定值,因此当NP+BQ取最小值时,
为定值,因此当NP+BQ取最小值时, ![]() 有最大值.如答图2所示,作点B关于直线AC的对称点B′,由分析可知,当B′、Q、F(AB中点)三点共线时,NP+BQ最小,最小值为线段B′F的长度.
有最大值.如答图2所示,作点B关于直线AC的对称点B′,由分析可知,当B′、Q、F(AB中点)三点共线时,NP+BQ最小,最小值为线段B′F的长度.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
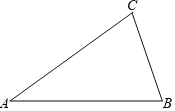
【题目】如图,△ABC的周长为20,其中AB=8,
(1)用直尺和圆规作 AB 的垂直平分线 DE 交 AC 于点 E,垂足为 D,连接 EB;(保留作图痕迹,不要求写画法)
(2)在(1)作出 AB 的垂直平分线 DE 后,求△CBE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013成都)若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC. 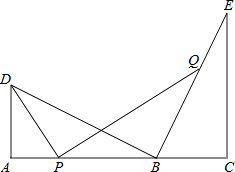
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q; (i)当点P与A、B两点不重合时,求 ![]() 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1= ![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论: ①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论: ①a= ![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
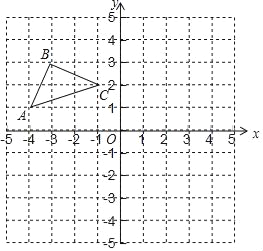
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com