
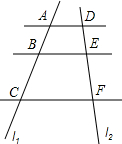
 如图,已知AD∥BE∥CF,若$\frac{AB}{BC}=\frac{2}{5}$,求$\frac{DE}{EF}$的值.
如图,已知AD∥BE∥CF,若$\frac{AB}{BC}=\frac{2}{5}$,求$\frac{DE}{EF}$的值. 科目:初中数学 来源: 题型:填空题
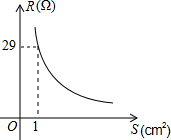 实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例,一条长为100km的铅导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为R=$\frac{29}{S}$;当S=2cm2时,R=14.5Ω.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例,一条长为100km的铅导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为R=$\frac{29}{S}$;当S=2cm2时,R=14.5Ω.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
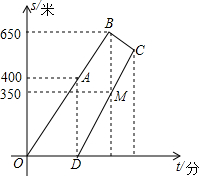 小明要在周日8点50分之前赶到距家1000米的书店去买书.早8点20分从家出发,8分钟后妈妈发现他忘了带钱包,于是立即出发按他走的路线去追.妈妈出发几分钟后,小明也发现了忘带钱包,于是按原路原速返回去取,几分钟后与妈妈相遇.假设在此过程中小明和妈妈的速度均保持不变,如图所示,给出两人离家距离s(米)和小明所走的时间t(分)之间的函数图象,结合图象回答下列问题:
小明要在周日8点50分之前赶到距家1000米的书店去买书.早8点20分从家出发,8分钟后妈妈发现他忘了带钱包,于是立即出发按他走的路线去追.妈妈出发几分钟后,小明也发现了忘带钱包,于是按原路原速返回去取,几分钟后与妈妈相遇.假设在此过程中小明和妈妈的速度均保持不变,如图所示,给出两人离家距离s(米)和小明所走的时间t(分)之间的函数图象,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
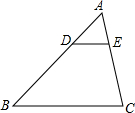 如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:
如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
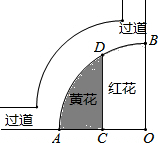 如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在$\widehat{AB}$上,CD∥OB,则图中种植黄花(即阴影部分)的面积是$\frac{8}{3}$π-2$\sqrt{3}$(结果保留π).
如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在$\widehat{AB}$上,CD∥OB,则图中种植黄花(即阴影部分)的面积是$\frac{8}{3}$π-2$\sqrt{3}$(结果保留π).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com