
【题目】如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G. 
(1)求证:BD∥EF;
(2)若点G是DC的中点,BE=6,求边AD的长.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵DF=BE,
∴四边形DBEF是平行四边形,
∴BD∥EF
(2)解:∵AD∥BC,
∴∠FDG=∠C,
∵点G是DC的中点,
∴DG=CG,
在△DGF与△CGE中,
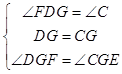 ,
,
∴△DGF≌△CGE,
∴DF=CE,
∵DF=BE=6,
∴EC=DF=6,
∴BC=BE+EC=12,
∵四边形ABCD是平行四边形,
∴AD=BC=12.
【解析】(1)根据平行四边的判定与性质,可得答案;(2)根据ASA证明△DGF≌△CGE,再根据全等三角形的性质与平行四边形的性质即可求解.
【考点精析】掌握平行四边形的性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1、l2相交于点A(2,3),直线l1与x轴交点B的坐标为(﹣1,0),直线l2与y轴交于点C,已知直线l2的解析式为y=2.5x﹣2,结合图象解答下列问题: 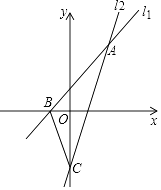
(1)求直线l1的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,2017年中哈铁路(中国至哈萨克斯坦)运输量达12800000,将12800000用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
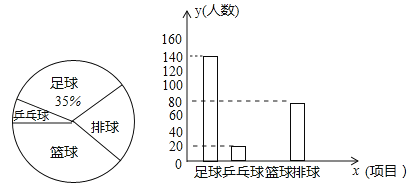
【题目】某校为提高学生身体素质,决定开展足球、篮球、台球、乒乓球四项课外体育活动,并要求学生必须并且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并绘制出以下两幅不完整的统计图.请根据统计图回答下列问题.(要求写出简要的解答过程)
(1)这次活动一共调查了多少名学生?
(2)补全条形统计图.
(3)若该学校总人数是1300人,请估计选择篮球项目的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com