
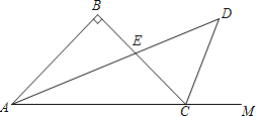
【题目】如图,在△ABC中,∠B=90°,AB=BC,∠BCM是△ABC的外角,∠BAC、∠BCM的平分线交于点D,AD与BC交于点E,若BE=2,则AEDE=____.
【答案】8![]() +8.
+8.
【解析】
作EF⊥AC于F,由角平分线的性质得出FE=BE=2,证出△CEF是等腰直角三角形,再根据勾股定理表示出AE,证出DE=DC,∠CDE=45°,作EM⊥CD于M,则∠MED=45°,作∠ECN=∠CEM=22.5°,则CN=EN,∠CNM=45°,则△MDE和△MCN是等腰直角三角形,得出ME=MD,MC=MN,设MC=MN=x,在Rt△MCE中,由勾股定理得出方程,解出x,即可得到答案.
作EF⊥AC于F,如图所示:
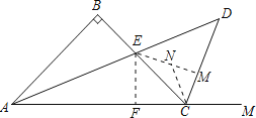
∵AD是∠BAC的平分线,∠B=90°,EF⊥AC于F,
∴FE=BE=2,
∵AB=BC,
∴∠BAC=∠ACB=45°,
∴∠BCM=135°,△CEF是等腰直角三角形,
∴FC=FE=2,CE=![]() FE=2
FE=2![]() ,
,
∴AB=BC=BE+CE=2+2![]() ,
,
∴AE=![]() =
=![]() =2
=2![]() ,
,
∵∠BAC、∠BCM的平分线交于点D,
∴∠CAE=![]() ∠BAC=22.5°,∠DCE=
∠BAC=22.5°,∠DCE=![]() ∠BCM=67.5°,
∠BCM=67.5°,
∵∠DEC=∠CAE+∠ACB=67.5°=∠DCE,
∴DE=DC,∠CDE=45°,
作EM⊥CD于M,则∠MED=45°,
∴∠CEM=67.5°-45°=22.5°,
作∠ECN=∠CEM=22.5°,
则CN=EN,∠CNM=45°,
则△MDE和△MCN是等腰直角三角形,
∴ME=MD,MC=MN,
设MC=MN=x,则EN=CN=![]() x,
x,
∴MD=ME=x+![]() x,
x,
在Rt△MCE中,由勾股定理得:x2+(x+![]() x)2=(2
x)2=(2![]() )2,
)2,
解得:x=![]() ,
,
∴DE=DC=(2+![]() )x=(2+
)x=(2+![]() )
)![]() ,
,
∴AEDE=2![]() (2+
(2+![]() )
)![]() =2(2+
=2(2+![]() )
)![]() =8
=8![]() +8;
+8;
故答案为:8![]() +8.
+8.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
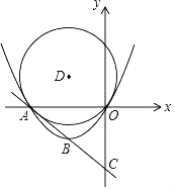
【题目】 已知:直线y=-x-4分别交x、y轴于A、C两点,点B为线段AC的中点,抛物线y=ax2+bx经过A、B两点,
(1)求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,连结AD、CD,问在抛物线上是否存在点P,使S△ACP=2S△ACD?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若E为⊙D上一动点(不与A、O重合),连结AE、OE,问在x轴上是否存在点Q,使∠ACQ:∠AEO=2:3?若存在,请求出所有满足条件的点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李通过对某地区1998年至2000年快餐公司发展情况的调查,制成了该地区快餐公司个数情况的条形图如图所示,和快餐公司盒饭年销量的平均数情况条形图,利用这些信息解答下列问题:


(1)1999年该地区销售盒饭共 万盒;
(2)该地区盒饭销量最大的年份是 个,这一年的年销量是 万盒;
(3)这三年中该地区每年平均销售盒饭多少万盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
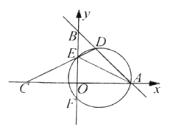
【题目】如图,在平面内直角坐标系中,直线y=-x+6分别于x轴、y轴交于A、B两点,点C与点A关于y轴对称,点E为线段OB上一动点(不与O、B重合),CE的延长线与AB交于点D,过A、D、E三点的圆与y轴交于点F
(1)求A、B、C三点的坐标
(2)求证:BE·EF=DE·AE
(3)若tan∠BAE=![]() ,求点F的坐标
,求点F的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨。梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°, AD=3m。
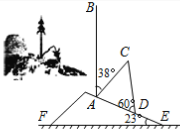
(1)求∠DAC的度数;
(2)求这棵大树折断前的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,G为AD上一点,连接BG,CG,作CE⊥BG于点E,连接ED交GC于点F.

(1)如图1,若点G为AD的中点,则线段BG与CG有何数量关系?请说理由.
(2)如图2,若点E恰好为BG的中点,且AB=3,AG=k(0<k<3),求![]() 的值(用含k的代数式表示);
的值(用含k的代数式表示);
(3)在(2)有条件下,若M、N分别为GC、EC上的任意两点,连接NF、NM,当k=![]() 时,求NF+NM的最小值.
时,求NF+NM的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台摄制组乘船往返于A码头和B码头进行拍摄,在A、B两码头间设置拍摄中心C.在往返过程中,假设船在A、B、C处均不停留,船离开B码头的距离s(千米)与航行的时间t(小时)之间的函数关系式如图所示.根据图象信息,解答下列问题:
(1)求船从B码头返回A码头时的速度及返回时s关于t的函数表达式.
(2)求水流的速度.
(3)若拍摄中心C设在离A码头12千米处,摄制组在拍摄中心分两组拍摄,其中一组乘橡皮艇漂流到B码头处,另一组同时乘船到达A码头后马上返回,求两摄制组相遇时离拍摄中心C的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐山独峰,倚天独立.身高1.6米的小明(GF)和身高1.8米的爸爸(HE)前去游览,山腰处的一棵缀满红叶的枫树(A)吸引了他们的目光,已知小明的仰角为30°,爸爸的仰角为45°,若小明与爸爸之间(EF)相距6米,求枫树(A)与地面的距离(AD)为多少米?(参考数据:![]() 1.41,
1.41,![]() 1.73,结果保留一位小数.)
1.73,结果保留一位小数.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com